Echtzeit Kollisionsvermeidung für einen Industrieroboter durch 3D-Sensorüberwachung

Andreas Bischoff

Inhalt

Abbildungsverzeichnis

Tabllenverzeichnis

Kapitel 1
Einführung

Moderne Fertigungstechnologien erfordern flexible Fertigungsverfahren, wie sie durch den Einsatz von Industrierobotern verwirklicht werden können. Die zunehmende Integration von Werkzeugmaschinen und Industrierobotern in Fertigungszellen erfordert die Entwicklung neuer Konzepte für kollisionsfreies Arbeiten mehrerer flexibler Komponenten.

Diese Arbeit stellt ein Konzept für die Echtzeit Kollisionsvermeidung für einen Indutrieroboter vor.

Der erste Teil dieser Arbeit beschäftigt sich mit der Realisation von Vorbedingungen, wie sie für eine Echtzeit-Bildverarbeitung notwendig sind. Zunächst wird ein Verfahren erläutert, welches geeignet ist, ein Stereokamera-System derart zu kalibrieren, daß eine zuverlässige und genaue Detektion von im Arbeitsraum des Industrieroboters auftauchenden Hindernissen ermöglicht wird.

Der zweite Teil dieser Arbeit beschäftigt sich mit dem Entwurf eines verhaltensbasierten Konzepts der Einflußnahme auf die Roboterbewegung. Eine Kollisionsvermeidungsstrategie wird entwickelt und in Form eines Fuzzy-Controllers realisiert.

Kapitel 2
Entwicklungsumgebung

Die für die Realisierung zur Verfügung stehenden Hard- und Softwarekomponenten werden im folgenden kurz beschrieben.

2.1  Hardware, Fertigunszelle und Bildverarbeitungskomponenten

Die eingesetzte Hardware besteht im wesentlichen aus dem Industrieroboter, der angeschlossenen Robotersteuerung, einem mit Bildverarbeitungskarten ausgestatteten VME ¹-Bus-System und einer Workstation für die Softwareentwicklung.

2.1.1  Überblick über die Fertigunszelle

Einen Überblick über die Fertigungszelle bzw. die Anordnung der Kameras gibt die Abbildung 2.1.

*0.9!

2.1.2  Der Industrieroboter PUMA 562

Bei dem UNIMATION Industrieroboter vom Typ PUMA 562 in der Fertigungszelle handelt es sich um einen Kombi-Arm-Roboter, der sechs Freiheitsgrade in der Bewegung aufweist.

Gelenk 1 schwingt um eine Achse, welche vertikal durch den Rumpf des Roboters verläuft. Gelenk 2 rotiert um eine Achse horizontal durch das Schulterstück und verläuft in einer lotrechten Bewegung zum Rumpf. Das dritte Gelenk rotiert um eine Achse, die parallel zur Gelenk-Achse 2 verläuft. Diese Bewegungen geben dem Arm drei Freiheitsgrade. Hinzu kommen die drei Freiheitsgrade der drei Einzelgelenke des Handgelenks. Die Bewegungen der Gelenke 4, 5 und 6 werden als "Rollen", "Steigung" und "Gierung" bezeichnet.

2.1.3  Die Robotersteuerung MARK3

Die angeschlossene Robotersteuerung UNIMATION MARK3 enthält die Regler für die einzelnen Roboterachsen und die Spannungsversorgung für die Gelenkmotoren. Außerdem ist ein Steuerrechner enthalten, welcher die Programmierung der Roboterbewegungen in der Programmiersprache VAL-II ermöglicht. Die Steuerung erlaubt den Anschluß eines Terminals zur Ein- und Ausgabe der Programme, eines Floppy-Disk-Laufwerkes zur externen Datenspeicherung und eines Teach-Zusatzgerätes zur Handsteuerung des Roboters. Zusätzlich kann ein externer Rechner über eine serielle RS422-Schnittstelle angeschlossen werden.

2.1.4  Überblick über die eingesetzte Bildverarbeitungshardware

Bei der eingesetzten Bildverarbeitungshardware handelt es sich im wesentlichen um ein VME -BUS-System, ausgerüstet mit einer Motorola 68040-CPU-Karte der Firma Microsys und speziellen Bildverarbeitungskarten der Firma Eltec. Zu Kommunikationszwecken ist der Rechner zusätzlich mit einer VME-BUS-Ethernetkarte ausgestattet. Bei den Bildverarbeitungskarten handelt es sich im einzelnen um jeweils zwei IC40 Einplatinencomputer mit integriertem Framegrabber, zwei Kantenverstärkungskarten vom Typ THINEDGE und zwei Vektorisierungkarten² vom Typ VECTOR.

2.1.5  Haupt-CPU-Karte

Die eingesetzte CPU-Karte verfügt über einen Motorola MC68040 Prozessor mit integriertem Floating Point Prozessor (FPU) und Memory Management Unit (MPU). Der Prozessor wird mit 25 MHz Takt betrieben, der Bustakt beträgt ebenfalls 25 MHz. Die Karte verfügt über 16 MB RAM (maximal 64 MB), einen integrierten NCR53C710 SCSI Controller und zwei asynchrone MC68681 DUART's mit vier seriellen Schnittstellen, welche jeweils für RS232, RS422 oder RS485 Pegel gejumpert werden können. Eine dieser seriellen Schnittstellen ist für den Anschluß eines Terminals vorgesehen, welches die Systemkonsole³ des Rechners darstellt. Außerdem verfügt die CPU-Karte über ein am sogenannten Piggyback-Connector ``huckepack'' angeschlossenes Microsys GRC06-Grafikboard und über eine 32 Bit VME-Bus Schnittstelle.[7]

2.1.6  IC40 Slave CPU mit integriertem Framegrabber

Die IC40 CPU ist ein Einplatinencomputer mit integriertem Framegrabber, welcher Videosignale von standard Videokameras digitalisieren und flimmerfrei auf Workstation-Monitoren ausgeben kann. Die integrierte Motorola 68040 CPU wird mit 25 MHZ Takt betrieben und zu kommunikationszwecken durch einen 68681 DUART Chip unterstützt. Die beiden seriellen Schnittstellen des DUART werden für einen Maus- und einen Tastaturanschluß genutzt. Die angelegten Videosignale müssen den Normen CCIR (625-Zeilen) oder EIA⁴ (525-Zeilen) entsprechen. Bis zu vier Kameras können an einer einzigen IC40 Karte angeschlossen werden, ein eingebauter Multiplexer erlaubt die Auswahl der zu digitalisierenden Videoquelle. Programmierbare Digitalisier-Frequenzen erlauben es, Daten in gleicher horizontaler und vertikaler Auflösung abzuspeichern (Vorteil für die Bildverarbeitung: Es ergeben sich quadratische Pixel). Eine ``Look Up Table'' (LUT⁵) mit 256 8-bit Einträgen kann für Grauwert-Transformationen genutzt werden. Zusätzlich zum VME-BUS, über den genauso, wie über die integrierte CPU auf alle Ressourcen der IC40 zugegriffen werden kann, verfügt die Karte über einen sogenannten Videobus (VIB) der eine pipeline-artige⁶ Kommunikation mit weiteren Bildverarbeitungskomponenten zuläßt.[8]

2.1.7   CCD Kameras

Bei den eingesetzten CCD-Kameras handelt es sich um schwarzweiß Kameras des Herstellers Hitachi, Modell KP-161. Die Kameras verfügen über einen Graustufen CCD-Sensor der Größe 4,85mm x 6.5 mm ² und liefern ein Videobild der Norm CCIR. Die Kameras verfügen über eine Schnittstelle zum Anschluß von Objektiven mit automatischer Blendeneinstellung. Diese Schnittstelle stellt für Objektive mit einer solchen Funktionalität eine Spannungsversorgung und ein Videosignal zur Verfügung.

2.1.7.1  Objektive

Die verwendeten Objektive verfügen über eine automatische Blendeneinstellung, welche abhängig vom Videosignal, eine konstante Grauwertverteilung regelt. Zwei Einstellregler erlauben die Justierung der Parameter der mittleren und der größsten Helligkeit für diese Grauwertregelung. Die Brennweite der Objektive beträgt 4,5-10mm.

2.1.8  Beleuchtung

In der hier beschriebenen Arbeitszelle werden zwei 2000 Watt Halogenstrahler eingesetzt, welche die von den Kameras beobachtete Szenerie indirekt beleuchten. Das regelungstechnische Labor verfügt zusätzlich über abdunkelbare Fenster, so daß eine konstante Beleuchtung gewährleistet werden kann.

2.1.9  Kantenextraktionskarten

Die eingesetzten Kantenverstärkungskarten der Firma ELTEC Modell THINEDGE sind Echtzeit-Bildverarbeitungsprozessoren für die Extraktion von rauschfreien Konturen aus Grauwertbildern. Die extrahierten Konturen sind 1 Bit breite (thinned=ausgedünnt) binäre Konturen ohne kritischen Schwellenwert. Zu jedem Konturpunkt wird ein korrespondierendes 8 Bit Winkel Attribut für die Kontur-Orientierung generiert. Die THINEDGE-Karten arbeiten als Pipeline-Prozessoren auf dem schon in Abschnitt 2.1.6 erwähnten Video-BUS. Sie verfügen außerdem über ein VME-BUS Interface, über das eine externe CPU Zugriff auf die internen Register und die ``look-up table'' (LUT), z.B. zu Initialisierungszwecken, ermöglicht wird. Im online Betrieb kommunizieren die THINEDGE-Karten ausschießlich über den Video-BUS. Ein integrierter 8 Bit DAC⁷ erlaubt den Anschluß eines Standart-Videomonitors (CCIR oder EIA-Norm) an die THINEDGE-Karten.[9]

2.1.10  Vektorisierer

Zur Vektorisierung des kantenverstärkten Videosignals werden VECTOR-VME-BUS Karten der Firma ELTEC eingesetzt. Die Eingabeinformation der VECTOR-Karten ist die Konturinformation und die lokale Orientierung der Kontur-Pixel, wie sie die THINEDGE-Karten über den Video-BUS zur Verfügung stellen. Die VECTOR-Karten konvertieren konturbasierte Bilder in eine symbolische Repräsentation. Diese symbolische vektorielle Beschreibung gleicht der in CAD-Anwendungen und spart Speicher und Verarbeitungszeit. Die Konvertierung erfolgt durch Approximation der Konturen durch gerade Linienelemente, die als Vektoren bezeichnet werden. Diese Vektoren werden in einem Symbol-Buffer mit maximal 2KByte Einträgen gepeichert. Dieser Buffer ist über den VME-BUS erreichbar und so von einem beliebigen VME-BUS-Master für die weitere Bearbeitung lesbar.

Die gesamte Kantenextraktion und Vektorisierung läuft in Video-Echtzeit ab. Bei Verwendung von einem CCIR-Videosignal kommt es höchstens zu einer Verzögerungszeit von 0.9 ms. Diese Verzögerungszeit ist unabhängig von der Komplexität der beobachteten Szene.[10]

2.1.11  Kontrollmonitore

Das Bildverarbeitungssystem ist mit insgesamt vier Kontrollmonitoren ausgestattet, von denen jeweils zwei an die IC40-Framegrabberkarten und die THINEDGE-Karten angeschlossen sind.

Bei den an die IC40-Karten angeschlossenen Geräten handelt es sich um Workstationmonitore mit RGB⁸-Eingängen. Diese Monitore zeigen die digitalisierten Grauwertbilder an. Die Geräte an den THINEDGE-Karten stellen das kantenverstärkte Bildsignal dar.

2.1.12  Entwicklungsrechner SUN Workstation

Der Hostrechner für die Cross-Entwicklungsumgebung ist eine SUN-Ultra Workstation mit einem ULTRA-SPARC Prozessor⁹, 167 MHz Taktfrequenz und 256 MB Speicherausbau. Auf dieser Workstation läuft das Betriebssystem SUNOS 5.5.1 mit der grafischen Benutzeroberfläche X11R6.

2.2  Software

Die eingesetzten Softwarekomponenten gliedern sich auf in Systemsoftware, d.h. Betriebssysteme, Treibersoftware und Entwickungssoftware (Editoren und Compiler). Hier sollen kurz die Eigenschaften des auf dem Bildverarbeitungssystem eingesetzen Echtzeit-Betriebssystem OS9 und die verwendeten Compiler erläutert werden. Eine fundierte Einführung in OS9 findet sich [12]. Auf den GNU-C-Crosscompiler für OS9 wird näher eingegangen, da dieser für das beschriebene Projekt von entscheidender Bedeutung ist. Zusätzlich eingesetzte Libraries für Bildverarbeitung und Fuzzy-Logik werden in den Kapiteln 5.3.1 und 7.2 beschrieben.

2.2.1  OS9

OS9 ist ein skalierbares Echtzeitbetriebssystem, welches multitasking- und multiuserfähig ist. Die Firma Microware entwickelte OS9 ursprünglich für den Motorola 6809 8-Bit-Prozessor in Maschinensprache und portierte es mit dem Aufkommen der moderneren 68000 16-Bit Prozessoren von Motorola auf diese Plattform. Diese Variante trägt die Bezeichnung OSK¹⁰und ist die heute am häufigsten eingesetzte. Microware entwickelte eine OS9-Variante, die zum großen Teil in C geschrieben ist, was relativ einfache Portierungen auf verschiedene Prozessorarchitekturen ermöglichte. So sind heute Portierungen beispielsweise für Intel X86 und Motorola Power-PC Architekturen verfügbar. OS9 ist stark modularisiert, was einerseits im Vollausbau ein UNIX-ähnliches, multiuserfähiges und mit grafischer Benutzeroberfläche ausgestattetes Host-Betriebssystem, andererseits ein massenspeicherloses kompaktes Betriebssystem für Embedded-Controller ermöglicht¹¹. Auf dem VME-BUS basierten Bildverarbeitungssystem wird die OS9-Version 2.3¹² eingesetzt.

2.2.2  Lokales OS9 auf den Slave CPU's

Die beiden lokalen 68040 CPU's auf den ELTEC-IC40 Framegrabberkarten werden ebenfalls unter OS9 betrieben. Diese CPU's verfügen über kein eigenes Massenspeicher-Filesystem, sondern verwalten ihren eigenen Hauptspeicher, können aber auch auf den VME-BUS zugreifen. Die Kontrollogik der IC40-Karten ermöglicht es der Haupt(Host)-CPU über ein Register sowohl den Videograbber zwischen einem sogenannten Live-Modus (kontinuierliche Akquisition) und dem Snapshot-Modus (einzelner Frame) umzuschalten, als auch Interrupts auf den IC40-CPU's zu generieren, um mit diesen zu kommunizieren¹³. Außerdem kann die Host-CPU die IC40-CPU's resetten, um dort einen definierten Betriebszustand herbeizuführen. Die IC40-Karten verfügen über Flash-Eprom¹⁴ in denen ein lokales Betriebssystem gepeichert werden kann. Alternativ kann auch ein Betriebssystem von der Host-CPU auf die IC40 heruntergeladen werden. Um eine größtmögliche Flexibilität zu gewährleisten, wurde die zweite Alternative gewählt. Das lokale OS9 wird dann direkt aus dem RAM der IC40 gestartet, und verfügt nur über die notwendigen Module zum Betrieb ohne Massenspeicher. OS9 durchsucht nach dem Start des Betriebssystems den verfügbaren Speicherbereich, unterscheidet diesen nach ROM und RAM und sucht nach gültigen Modulen, welche mittels eines speziellen Synchronisationswortes (4AFCh) von anderen Speicherbereichen zu unterscheiden sind. Der OS9 Memory-File-Manager (mfm) ermöglicht ein lokales Filesystem im RAM, vergleichbar mit einer RAM-Disk.

2.2.2.1   Kommunikation Host- Slave CPU's

Das OS9-Betriebssystem der Host- und Slave-CPU's verfügt über einen Devicetreiber, der auf der Host-CPU ein Character-Device¹⁵ (zeichenorientiert) implementiert, über welches Standard-Ein- und Ausgabe der Slave-CPU's abgewickelt werden können. Der Befehl ``talk ic_1'' verbindet beispielsweise das aktuelle Terminal mit der Standard-Ein- und Ausgabe der ersten IC40-Karte über das Device ``ic_1'', dessen Devicetreiber im Modulverzeichnis liegt. Die Funktionalität von ``talk'' ist in etwa vergleichbar mit ``telnet'', welches eine Terminalemulation über ein Netzwerk bereitstellt. Weitere Befehle zur Steuerung der Slave-CPU's über die Host-CPU sind:

2.2.3  Microware Entwicklungsumgebung

Auf dem einzusetzenden VME-BUS-System läuft MICROWARE OS-9, erweitert um ein TCP/IP-Paket der Firma N.A.T., welches Telnet, FTP (File Transfer Protokoll) und NFS-Client- und Server-Funktionalitäten zur Verfügung stellt. Als grafische Benutzerumgebung dient eine eingeschränkte, an OS-9 angepaßte Version von X-Windows.

MICROWARE liefert mit OS9 den MICROWARE C-Compiler, einen Linker und Binder, ein Make-Utility und den Source-Level-Debugger aus. Der Standard-Editor des Systems ist eine OS9-Portierung des MICROEMACS.

2.2.3.1  Der Kernigham Ritchie Microware C-Compiler

Da der mitgelieferte C-Compiler nur den alten Kernigham Ritchie C-Standard und nicht den aktuellen ANSI-C Standard unterstützt, ist dieser Compiler für die Einbindung ANSI-C kompatibler Softwaremodule, wie beispielsweise das in Abschnitt 5.3.1 beschriebene Bildverarbeitungslibrary, ungeeignet.

Zusätzlich steht mit dem ANSI-C kompatiblen ULTRA-C noch ein zweiter C-Compiler von Microware zur Verfügung, allerdings ist die vorhandene frühe ULTRA-C-Version noch in einigen Komponenten fehlerbehaftet.

2.2.4  Der Microware Source-Level-Debugger

Auf dem OS-9-Rechner steht der Microware Source-Level-Debugger zur Verfügung, der nicht nur vom Microware-C-Compiler, sondern ebenfalls durch den GNU-C- und den im Abschnitt 2.2.6 beschriebenen Crosscompiler unterstützt wird. Remote-Debugging, z.B. ein Debugger-Aufruf über das Netzwerk, unterstützt der Microware Source-Level-Debugger leider nicht.

2.2.5  GNU-C-Compiler

Aus diesem Grund stellte sich die Frage, ob nicht zusätzlich freie Software zur Entwicklung herangezogen werden sollte. Eine umfangreiche Recherche im Internet bzw. im Use-Net nach freier Software für OS9[4] führte zu den OS9-Portierungen der GNU¹⁶-Utilities.

Der GNU-C/C++-Compiler "gcc" ist wohl das bekannteste GNU-Produkt und stellt einen sehr portablen, leistungsfähigen und ausgezeichnet dokumentierten Compiler zur Verfügung. Die Portierung der Version 2.6 des GNU-Compilers auf OS9 von Stefan Paschernag[5] ist der leistungsfähigste, momentan verfügbare C-Compiler für OS9.

2.2.6   GNU-C-Crosscompiler¹⁷

Umfangreichere Software-Projekte mit mehreren tausend Zeilen Quellcode sind in ihrer Entwicklungsgeschwindigkeit stark abhängig von der Dauer der Entwicklungszyklen, d.h. der Zeit, welche zwischen einer Änderung des Quellcodes und der Möglichkeit des Tests einer solchen Modifikation mit dem erfolgreich compiliertem Programm vergeht. Solche ``Turn-Around''-Zeiten sind im Interesse einer zügigen Softwareentwicklung möglichst zu minimieren. Das eingesetzte Microware VME-BUS-Entwicklungssystem ermöglicht keine drastische Verkürzung der Entwicklungszyklen mehr, weil nur noch ein schnellerer Prozessor,¹⁸ der auf den Microware-Boards eingesetzten Motorola-CPU-Familie zur Verfügung steht. Motorola entwickelt zukünftig nur noch die neue Power-PC basierte CPU-Familie weiter. Ein weiterer gangbarer Weg zur Verkürzung der Entwicklungszyklen ist der Einsatz eines Crosscompilers.

Ein Crosscompiler ist ein Compiler, der Quellcode einer Programmiersprache auf einer Rechnerarchitektur übersetzen kann die nicht die Zielarchitektur ist. Das auf dem Host-Rechner compilierte Programm ist nur auf dem Zielrechner (Target) ausführbar, der über eine andere Prozessorarchitektur und/oder über ein anderes Betriebsystem verfügen kann.

Unter Anderem ergeben sich folgende Vorteile beim Einsatz eines Crosscompilers:

1. Compilierungsgeschwindigkeit:
   Die Übersetzungsgeschwindigkeit erhöht sich, wenn der Host wesentlich schneller ist als das Target. In diesem speziellen Fall sind die beiden ULTRA-SPARC Prozessoren der Host-Maschine um mehr als eine Zehnerpotenz schneller als der 68040 Prozessor der Zielmaschine.
2. Stabilität:
   Z.B. Die mitgelieferten ELTEC IC40 Utilities erfordern die Abschaltung der integrierten MMU der 68040 CPU um im Usermode Zugriffe über den VME-Bus zu ermöglichen. Ein durch einen Programmierfehler verursachter versehentlicher Zugriff auf einen Speicherbereich, der von Systemprogrammen verwendet wird, führt zwangsläufig zum Absturz des gesamten Entwicklungssystems. Die Stabilität der Entwicklungsumgebung wird drastisch erhöht, wenn das Kompilat im Testlauf nicht auf der Entwicklungsmaschine (Host) läuft.
3. Kompatibilität:
   Der native GNU-C-Compiler für OS9 verwendet die originalen Programmiertools von Microware OS9. Diese Tools, z.B. der Linker und das Make-Utilitie, unterscheiden sich in ihrer Bedienung und ihren Kommandozeilenoptionen stark von UNIX bzw. GNU-Tools, so daß vorhandene Makefiles stark abgeändert werden müssen. Außerdem unterscheidet sich das TEXT-Dateiformat von OS9 von dem unter UNIX eingesetzten Format. Zeilenenden werden mit CR quittiert, während unter UNIX LF verwendet wird. Also können beim Einsatz eines Crosscompilers vorhandene UNIX-ANSI-C-Quellcodeprojekte ohne große Modifikationen der Quelltexte und der Makefiles portiert werden. Die Portierung erfordert dann im günstigsten Fall nur noch die Anpassung der verwendeten Libraries bzw. Headerfiles.
4. Verfügbarkeit des Zielsystems:
   Das Zielsystem für die Crosskompilation muß physikalisch nicht zur Verfügung stehen. Dieser Punkt ist von besonderer Bedeutung für die Entwicklung von Software für Betriebsysteme, die auf mehreren Hardwarearchitekturen verfügbar sind. Linux und Windows NT sind beispielsweise außer für Intel-CPU basierte Systeme auch für Motorola-PowerPC und DEC-Alpha basierte Systeme verfügbar. Der Einsatz eines Crosscompilers erübrigt dann, bei Entwicklung für alle verfügbaren Plattformen des Betriebssystems, die Anschaffung der entsprechenden Zielplattform. Ebenso kann für Prozessoren, die noch gar nicht in Stückzahlen existieren, durch den Einsatz von Crosscompilern bereits Software entwickelt werden.
5. Verfügbarkeit einer Entwicklungsumgebung auf dem Zielsystem:
   Zielsysteme für bestimmte spezielle Anwendungen, wie z.B. Embedded-Controller verfügen gar nicht über eigene Entwicklungssysteme, da diese Zielsysteme aufgrund ihrer eingeschränkten Ressourcen (z.B. Speicher, IO-Interfaces) keinen Betrieb eines Entwicklungssystems auf dem Target ermöglichen. Auch für Prozessoren für die noch gar keine, bzw. keine Entwicklungsumgebung mehr existiert, kann durch den Einsatz von Crosscompilern Software entwickelt werden.

All diese Vorteile, insbesondere der um Faktoren schnellere Entwicklungszyklus, bedingt durch kürzere ``Turn-Around''-Zeiten bei der Compilierung lassen die Verwendung eines Crosscompilers geeignet erscheinen.

Es existieren verschiedene kommerzielle Crosscompiler für OS9, unter anderem von Microware selbst und der Firma Metrowerks, die eine Entwicklungsumgebung für verschiedene Zielsysteme anbietet, zu denen auch OS9 zählt. Diese beiden Lösungen sind sehr teuer und jeweils an festgelegte Host-Plattformen gebunden.¹⁹

Zwei freie Alternativen zu diesen kommerziellen Crosscompilern sind der OS9exec, der leider nur für Apple-Macintosh Host-Systeme verfügbar ist, und der schon erwähnte GNU-C-Compiler der auch als Crosscompiler eingesetzt werden kann. Die schon erwähnte Qualität und Verfügbarkeit für verschiedene Plattformen des GNU-C-Compilers sind die entscheidenden Kriterien zur Auswahl dieses Crosscompilers für dieses Projekt.

2.2.6.1  Besonderheiten des GNU-Crosscompilers für OS9

Unglücklicherweise läßt sich kein nativer GNU-C-Compiler aus den offiziellen Sourcen für OS9 bauen. Die von Stephan Pascherdag vorgenommene Portierung fand keinen Einzug in die aktuellen Quellen des gcc. Ebenso ist die einzige verfügbare Version des xgcc für OS9 ein ``Hack-Projekt'', welches leider keine Änderungen in den offiziellen gcc-Quellen hervorgerufen hat, weil es niemals komplett beendet wurde.

Die Portierung von Walter Hunt[1] der Version 2.6.2 des GNU-Compilers enthält Debug-Unterstützung für den MICROWARE Source-Level-Debugger, welche dem nativen GNU-C-Compiler für OS9 von Stephan Paschedag (Portierung des gcc 2.5.8) entnommen worden ist, allerdings werden OS9 spezifische Compilerswitches²⁰ des nativen gcc 2.5.8 nicht unterstützt. Die Portierung ist zu ca. 90% abgeschlossen²¹, die Floating-Point-Unterstützung funktioniert in der von Walter Hunt zur Verfügung gestellten Version noch nicht zuverlässig. Erst im Laufe des in dieser Arbeit beschriebenen Projektes veröffentlichte Carl Kreider[2] nach einer Diskussion dieses Themas im USENET²² Patches²³, die einen erfolgreichen Einsatz des Crosscompilers zuließen.

2.2.6.2  Vorbereitungen zum Build²⁴ des gcc-m68k-osk Crosscompilers

Der GNU-C-Compiler läßt sich schon in seiner Standarddistribution als Crosscompiler konfigurieren. Allerdings müssen für den Einsatz des gcc als Crosscompiler alle Headerfiles und binären Libraries auf das Hostsystem kopiert werden. Nach der Extraktion der gcc-Quellen, die inklusive der benötigten Quellen für die Binutilities²⁵ ca. 50 MB Festplattenplatz benötigen²⁶, müssen zunächst die Binutilities für den Einsatz eines Crosscompilers konfiguriert werden²⁷.

2.2.6.3  Konfigurationsnamen

Der Konfigurationsname und das Zielverzeichnis muß für alle Komponenten des Crosscompilers festgelegt werden. Der Konfigurationsname ist nötig um das Binary des Crosscompilers vom Binary des eventuell vorhandenen nativen GNU-C-Compilers auf dem Hostsystem zu unterscheiden. Die Konfigurationsnamen folgen dem Schema ``CPU-Hersteller-Betriebssystem'', beispielsweise ``rs600-ibm-aix'' und im hier beschriebenen Fall
``m68k-unknown-osk'', was für den Hersteller ``unknown'' mit ``m68k-osk'' abgekürzt werden kann. Die so konfigurierten Binaries heißen dann beispielsweise ``gcc-m68k-osk'', ``ld-m68k-os9'' usw.

2.2.6.4  Verzeichnisse für Libraries und Headerdateien

Der GNU-Crosscompiler benötigt auf dem Host-System die Header-Dateien und Libraries des Zielsystems. Um die Dateien von den nativen Versionen des Host-Systems zu unterscheiden, werden sie in die Verzeichnisse
<prefix>/<target>/include/ und <prefix>/<target>/lib/ kopiert, wobei <prefix> ein Verzeichnis ist, in das die Crosscompiler-Umgebung installiert werden soll. Die Voreinstellung für <prefix> ist /usr/local. Die Einstellung für <target> korrespondiert mit dem beschriebenen Konfigurationsnamen. Somit ergibt sich zum Beispiel folgender Pfad für die original OS9-Headerfiles auf der Host-Entwicklungsmaschine:
/DISK/E/bischoff/os9/usr/local/m68k-os9/include/,
mit <prefix> = /DISK/E/bischoff/os9/usr/local und
<target> = /m68k-os9.

Die originale OS9-Libraries müssen per FTP²⁸ im binär Modus, die Headerfiles im Text-Modus auf die Host-Maschine übertragen werden, weil das Text-Format von OS9 sich von dem unter UNIX unterscheidet. (Siehe Abschnitt 3)

2.2.6.5  Floating-Point-Unterstützung float.h

Für die Unterstützung von Fließkommaarithmetik benötigt der gcc eine Header-Datei float.h im Verzeichnis
<prefix>/lib/gcc-lib/<target>/<version>/include. Diese während der Übersetzung vom Makefile mittels Testprogramm erzeugte Header-Datei beschreibt die Fließkommaeigenschaften des Systems. Allerdings funktionieren diese Testprogramme nur beim Bau eines nativen GNU-C-Compilers, weil in diesem Fall Host- und Zielmaschine identisch sind. Beim Build eines Crosscompilers wird durch das Makefile die Warnung ausgegeben, daß es nicht möglich ist auf dem Zielsystem Testprogramme auszuführen. Der Benutzer muß eine geeignete float.h für das Zielsystem zur Verfügung stellen.

Im günstigsten Fall stellt das Zielsystem schon eine float.h eines gcc bereit, ansonsten muß das Programm enquite.c aus den gcc-Quellen auf dem Zielsystem ohne Optimierungen übersetzt werden. Wenn auch diese Möglichkeit nicht besteht ist eine float.h eines möglichst ähnlichen Betriebssystems, welches auf der Zielprozessorplattform läuft, auszuwählen. Im vorliegenden Fall wurden die unter OS9 vorliegende float.h verwendet, da enquire.c sich nicht ohne weiteres auf OS9 kompilieren läßt.

2.2.6.6  Floating-Point-Unterstützung libgcc1.a

Das libgcc1.a-Library enthält mathematische Funktionen, die der GNU-C-Compiler selbst während des Builds benötigt. Beim Bau eines nativen Compilers wird dieses Library von dem Compiler erzeugt, der zum compilieren des GCC eingesetzt wird. Dieser Compiler hat natürlich Kenntnis über die Fließkommafunktionalität des Systems (hier ist wieder das Hostsystem identisch mit dem Zielsystem), während beim Bau eines Crosscompilers diese Informationen fehlen.

Auch hier muß der Benutzer für eine passende libgcc1.a sorgen. Je nach Target-Maschine ergeben sich mehrere Optionen:

1. Keine Fliekommaunterstützung wird benötigt:
   Wenn keine Floating-Point-Unterstützung benötigt wird, kann das libgcc1.a einfach als Stub-File angelegt werden.
2. Die Zielmaschine stellt bereits ein Floating-Point-Library zur Verfügung:
   Alle benötigten mathematischen Funktionen während des Builds können aus dem vorhandenen Floating-Point-Library aufgelöst werden. Für das libgcc1.a muß der Benutzer im File libgcc1.c entsprechende Makros erzeugen, welche die entsprechenden Funktionen auf das vorhandene Floting-Point-Library abbildet.
3. Auf der Zielmaschine existiert eine Entwicklungsumgebung, die in der Lage ist den gcc nativ zu übersetzen:
   Auf der Zielmaschine werden die gcc-Quellen mit ./configure -host <host> -target <target> konfiguriert, und dort wird dann lokal das liggcc1.a mit make libgcc1.a erzeugt und auf die Zielmaschine kopiert.
4. Nur wenige, einfache Funktionen, wie die Multiplikation und Division können auf der Zielmaschine nicht per vorhandener FPU aufgelöst werden:
   Nur einfache Makros für Multiplikation und Division müssen in das File liggcc1.c integriert werden.
5. Die Zielarchitektur verfügt über alle Floating-Point-Funktionen in der FPU und diese wird vom gcc unterstützt:
   In diesem Fall ist keine libgcc1.a nötig, das Makefile erkennt diesen Fall und überspringt die Generierung der Floating-Point-Library.
6. Die Zielarchitektur verfügt über keine FPU:
   Dieses ist beispielweise bei dem Motorola M68000 der Fall. Hier muß der Benutzer für eine geeignete Emulation der mathematischen Funktionen in der libgcc1.c selber sorgen. Für einige Embedded Controller steht eine lebgcc1.a fertig kompiliert zur Verfügung

2.2.6.7  Build der Binutilities und des gcc-m68k-osk Crosscompilers

Folgende Kommandos müssen ausgeführt werden um den Bau des Crosscompilers zu starten:

./configure --prefix=/DISK/E/bischoff/os9/usr/local 
--host=sparc-sun-sunos4.1.3 --target=m68k-os9 
--with-gnu-as --with-gnu-ld --enable-bfd-assembler 
--norecursion

2.2.6.8  Laufzeitvergleich gcc nativ OS9 mit gcc_m68k_osk auf SUN-Host

Nach erfolgreichem Build des xgcc wurde zum Laufzeitvergleich ein etwa 3500 Quelltextzeilen großes Projekt jeweils mit dem nativen gcc des OS9-Systems und dem erzeugten Crosscompiler auf dem Host-System übersetzt. Gemessen wurde die Übersetzungzeit inklusive Assembler und Linkeraufruf.

Es zeigt sich ein deutlicher Performancevorteil des xgcc von über zwei Zehnerpotenzen gegenüber dem nativen gcc unter OS9. Selbst wenn die nötige Übertragungszeit per FTP auf die Zielmaschine von ca. 5 Sekunden berücksichtigt wird, lohnt sich der Einsatz des xgcc enorm.

2.2.7  Entwicklungsumgebung auf der SUN-Workstation

 Auf dem Host-Rechner steht eine vollständige UNIX-Entwicklungsumgebung mit grafischer Benutzeroberfläche X-Windows zur Verfügung. Da für diese Architektur eine große Anzahl freier Editoren zur Verfügung steht, kann mit XEMACS ein mächtiger Editor mit umfangreichen Funktionen ausgewählt werden.

2.2.8  Die in XEMACS hervorragend integrierte Entwicklungsumgebung

Der XEMACS-Version 19.2[3] läßt sich hervorragend als integrierte Entwicklungsumgebung einsetzen, weil es unter anderem RCS-Versionkontrolle, Syntax-Highlighting und Compileraufruf auf den Benutzermenüs erlaubt. Compilermeldungen werden in einem separaten Fenster angezeigt, von angezeigten Fehlermeldungen wird direkt in die betreffenden Stellen im Quellcode verwiesen. Gemeinsam mit dem Crosscompiler ergibt sich mit der XEMACS ein großer Produktivitätsvorteil gegenüber der spartanischen Entwicklungsumgebung auf dem OS9-System.

Kapitel 3
Kommunikation mit der Robotersteuerung 

Auf das verwendete Kommunikationsprotokoll zwischen dem Bildverarbeitungsrechner und der Industrierobotersteuerung soll hier nur kurz eingegangen werden, da dieses Protokoll in [11] und [34] bereits ausgiebig erläutert wurde.

Die MARK3-Robotersteuerung ist mit einer seriellen RS422 Schnittstelle ausgestattet, die über einen RS422 nach RS232 Schnittstellenwandler mit dem Bildverarbeitungsrechner verbunden ist. Die auf der Robotersteuerung ablaufende Roboterprogrammiersprache VAL-II erlaubt über die sogenannte ALTER-Schnittstelle einen Modus, in dem die programmierte Bahn durch extern überlagerte Daten verändert wird. Diese Software-Schnittstelle wird verwendet um der Robotersteuerung Bewegungssteuerungs-Befehle zu übermitteln und die aktuelle Position des Roboters aus der Steuerung auszulesen. Die Kommunikation wird jeweils von der Robotersteuerung initiiert, während der Bildverarbeitungsrechner in einer definierten Zeitspanne auf die Datenpakete der Steuerung reagieren muß. Im laufenden Betrieb muß der Bildverarbeitungsrechner alle 28 ms einen Kommunikationszyklus durchführen wobei eine Reaktionszeit von maximal 15-17 ms (abhängig vom gewählten ALTER-Kommunikationsmodus, siehe [11]) auf eine Kommunikationsanforderung eingehalten werden muß.

Diese Randbedingungen machen den Einsatz eines echtzeitfähigen Betriebssystem erforderlich. Zusätzlich zu diesen Kommunikationsaufgaben muß die MICROSYS-CPU-Karte noch die Kommunikation mit den Bildverarbeitungskarten und die eigentliche softwareunterstützte 3D-Bildverarbeitung durchführen.

Um diese Funktionalitäten in Echtzeit zu gewährleisten wurden zwei Programmodule realisiert, die mit unterschiedlichen Prioritäten ihre Aufgaben wahrnehmen und sich per Interprozeßkommunikation miteinander koordinieren. Diese Interprozeßkommunikation ist über ein OS9-Datenmodul realisiert, ein Datenbereich auf den mehrere Prozesse zugreifen dürfen und der deshalb durch geeignete Synchronisationsmechanismen wie Semaphoren geschützt wird. Solche Synchronisationsmechanismen des Echtzeitbetriebssystems OS9 werden extensiv in [13] und [12] erläutert.

Der für die Kommunikation mit der Robotersteuerung vorgesehene Prozeß muß harten Echtzeitanforderungen genügen und läuft daher mit der höchsten Priorität. Er enthält aus Geschwindigkeitsgründen den im Abschnitt 3.1 beschriebenen Bahninterpolator und ist bis auf diesen im wesentlichen mit dem in [11] beschriebenen Kommunikationsprozeß identisch. Dieser Prozeß ,,schläft'' allerdings in den Zeiten in der die Robotersteuerung ein Daten-Paket verarbeitet und ein neues generiert. So bleibt ausreichend Rechenzeit für den eigentlichen Bildverarbeitungsprozeß übrig, der die in Abschnitt 5 erläuterte Stereobildverarbeitung, die Kommunikation mit den Bildverarbeitungskarten (siehe Abschnitt 4.10), die Fuzzy-Kollisionsvermeidungsalgorithmen (Abschnitt 7.3) und das Benutzerinterface
(Abschnitt 8) beinhaltet.

3.1   Ein einfacher Bahninterpolator für die ALTER -Schnittstellen der VAL-Robertersteuerung

Kollisionsvermeidungsalgorithmen (siehe Abschnitt6) benötigen für die Generierung eines günstigen Ausweichkurses um ein Hindernis Kenntnis des Ziels der aktuellen Bewegung. Da die ALTER-Software-Schnittstelle der Roboterprogrammiersprache VAL2 nur die Ausgabe der aktuellen Position des Roboters, nicht aber der Zielkoordinaten des aktuellen Bewegungssatzes ermöglicht, muß der externe Steuerungsrechner, also das Bildverarbeitungssystem, über die ALTER-Schnittstelle nicht nur die Ausweichbewegungen bei einer drohenden Kollision, sondern auch die ,,normale'' Bewegungsteuerung durchführen.

Zu diesem Zweck wurde eine einfache Bahninterpolation implementiert, die im Zusammenspiel mit der Möglichkeit Kurse zu teachen³⁰ und zu laden, eine simple Möglichkeit der Roboterprogrammierung ergibt.

Kapitel 4
2-D-Bildverarbeitung

Während jeder sehende Mensch eine genaue Vorstellung davon hat was ein Bild ist, werden die notwendigen Schritte für eine maschinelle Bildverarbeitung³¹ erst ersichtlich wenn man den biologischen Vorgang des Sehens mit den für die gleiche Funktionalität notwendigen künstlichen Verfahren vergleicht. Diffuses und gerichtetes Umgebungslicht wird von Objekten reflektiert, und wird in der Linse des Auges gebündelt und auf die Netzhaut projiziert. Die Muskulatur der Linse des Auges sorgt dafür, daß die Brennweite so einstellt wird das ein scharfes Bild auf der Netzhaut entsteht. Die Iris regelt die einfallende Lichtmenge, ähnlich wie eine Blende, um eine Anpassung an die Umgebungslichtstärke zu ermöglichen.

Zusätzlich können die Augen durch die Augenmuskulatur bewegt werden um verschiedene Objekte zu fixieren. Die Netzhaut besteht aus Nervenzellen, welche schon eine gewisse Vorverarbeitung der Bildinformation leisten und verschieden starke elektrische Signale an das Gehirn weitergeben. Eine umfassende Beschreibung der Vorgänge im menschlichen Auge findet sich in [27].

Im Gehirn werden die übermittelten Signale verarbeitet und die notwendigen Muskelbewegungen für die Iris, die Linsenverstellung und die Augenbewegungen koordiniert. Verschiedene Objekte werden im Gehirn aufgrund ihrer Helligkeitunterschiede und Farben unterschieden, ihre Ausdehnung wird ermittelt und die Bildinformation der beiden Augen wird miteinander verglichen um Korrespondenzen, also sich gleichende Punkte, in den Bildern einander zuzuordnen. Das Gehirn extrahiert aus den beiden Bildern räumliche Informationen.So wird eine Repräsentation der Umwelt, ein Modell und eine Interpretation der umgebenden Objekte erzeugt. Die vom Gehirn verarbeiteten Bilder sind Einzelbilder eines optischen Flusses, in denen eine Beziehung der Einzelbilder zu ihrer zeitlichen Abfolge vorgenommen werden. So können Bewegungen wahrgenommen werden, das heißt Objekte in Bildfolgen identifiziert werden. Diese Bearbeitungschritte führen zu einer massiven Datenreduktion. Die Anfangs große ungeordnete und rohe Bildinformation wird im Zuge der Bearbeitung auf wesentliche Informationen reduziert.

All diese Vorgänge laufen unbewußt ab, so daß einem sehenden Menschen diese Bildverarbeitung völlig trivial erscheint. In Wirklichkeit laufen verschiedene Prozesse der Informationsverarbeitung in verschiedenen Abstraktionsstufen ab. Die Disziplin der Bildverarbeitung versucht diese Fähigkeiten des Menschen und der Tiere künstlich nachzubilden. Einige dieser Mechanismen erfordern ein Bildverstehen, also Intelligenz, weshalb sich auch der Forschungszweig KI (Künstliche Intelligenz) mit Bildverarbeitung beschäftigt.

Praktische Anwendungsbereiche für Bildverarbeitungstechnologien lassen sich in allen Bereichen der Forschung, zum Beispiel für die automatische Auswertung von Bildern, der Medizin und in der Industrie finden. Für den Bereich der automatischen Auswertung von Bildern lassen sich beispielsweise die Farbbildauswertung, die automatische Entzerrung von Bildern, die Bildverbesserung und Rekonstruktion und die Verarbeitung nicht sichtbarer Spektralbereiche nennen. Durch hohe Verarbeitungskapazitäten wird auch eine Analyse von Bildfolgen möglich. Im Bereich der Medizin sind vor allen Dingen die Visualisierungstechniken der Comutertomographie zu nennen, die im Bereich der Diagnostik zu revolutionären Verbesserungen geführt haben. Auf die Anwendungsbereiche der industriellen Bildverarbeitung in der Automatisierungstechnik wird hier umfassender eingegangen.

4.1  Anwendungsbereiche der industriellen Bildverarbeitung

Die moderne Fertigunstechnologie entwickelt sich in Richtung Humanisierung der Arbeitswelt und Erhöhung der Produktqualität. Dieses führt zu einer Verbesserung der Nutzung vorhandener Produktionseinrichtungen und dadurch zur Steigerung des Automatisationsgrades.

In der industriellen Bildverarbeitung werden Bildsensortechniken für die Sichtprüfung, die Handhabung von Werkstücken, die Steuerung und Regelung von Maschinen und Prozessen und zur Überwachung von Maschinen und Arbeitsräumen eingesetzt. Funktionen von Bildsensoren sind in diesem Bereich die Prüfung auf Vollständigkeit, die Vermessung von Position und Ausmaßen, die Bestimmung von Formen und die Bestimmung von Oberflächeneigenschaften von Werkstücken [6]. Beispiele dieser Bereiche sind die Oberflächenprüfung verschiedener Materialien, wie Metallen, Kunststoffen, Lackflächen usw. auf Rauhigkeit, Textur und Verschmutzung. Ebenso gehört das Zählen von Objekten und das Vermessen von Abständen und Durchmessern für die Verpackungs- und Bestückungskontrolle, der Kontrolle von analogen und digitalen Anzeigeinstrumenten und die Materialprüfung zur Lokalisierung von Rissen und Lunkern, zu den Anwendungsbeispielen dieser Verfahren. [27]

Zum Bereich der Überwachung von Arbeitsräumen gehört die Kollisionsvermeidung von Industrierobotern der im Abschnitt 6genauer erläutert wird. Die Entwicklung von sehenden Industrierobotern ist nicht nur für Zwecke der Kollisionvermeidung interessant, sondern auch für flexible Handhabungsfähigkeiten, wie das Nachführen von Werkzeugen, Schweißelektroden, Schraubern und Bohrern. Die Bildverarbeitung wird hier eingesetzt, zur Lagebestimmung, Identifizierung und Sortierung von Objekten mit Hilfe durch diese Informationen gesteuerte Roboter.

Ziel dieser Verfahren ist unter anderem die Funktionalität "Griff in die Kiste" zu erreichen, die automatische Entnahme des jeweils obersten Objekts aus einem Behälter, wobei die Objekte verschiedenartig sein dürfen und ungeordnet übereinanderliegen dürfen. Die Lösung dieses Problems erfordert räumliches Sehen mit Erkennung von Verdeckungen und Schattenwürfen.

4.2  Komponenten der Bildverarbeitung

Im folgenden wird die Funktionalität der Bildverarbeitungskomponenten erläutert.

Die erste Stufe der Bildverarbeitung stellen die CCD-Kameras dar. Der beleuchtete Arbeitsraum wird über ein Objektiv auf den CCD-Sensor der Kamera abgebildet. Die Weiterverarbeitung erfolgt in den Schritten, Digitalisierung³², Kantenextraktion, Vektorisierung und softwaremäßiger 2-D- und 3-D-Bildverarbeitung.

4.3  Beleuchtungsmethoden

Für Bildverarbeitungszwecke spielt die Auswahl einer geeigneten konstanten Beleuchtung eine entscheidende Rolle. Anders als das menschliche Auge ist die Lichtempfindlichkeitscharakteristik von CCD-Sensoren nicht logarithmisch sondern proportional der Helligkeit. Während menschliche Augen aus diesem Grund auch bei schlechten Beleuchtungsverhältnissen in der Lage sind Kontrastunterschiede wahrzunehmen, sind CCD-Sensoren auf konstante und gute Ausleuchtung angewiesen. Schattenkonturen können ebenso wie Reflexkonturen nach dem Einsatz von Kantenverstärkungsverfahren nicht mehr von den eigentlichen Konturen der zu vermessenden Objekte unterschieden werden, deshalb ist einen intensive, konstante und indirekte, also diffuse Beleuchtung vorzuziehen.

Andere Anwendungen als die hier beschriebene setzen völlig andere Beleuchtungsverfahren voraus. Zum Beispiel erfordert das sogenannte Lichtschnittverfahren³³ein schmales Lichtband, daß z.B. mit einem durch einen ausgeweiteten Laserstrahl erzeugt werden kann.

4.4  Die Kameraoptiken

Die Brennweite als das entscheidende Kriterium für die Auswahl von Kameraobjektiven ist abhängig von den Gegebenheiten des zu überwachenden Arbeitsvolumens. Soll der Arbeitsraum vollständig erfaßt werden und ist der mögliche Beobachtungsabstand (die Bildweite), wie im beschriebenen Fall bei Anordnung der Kameras oberhalb des Arbeitsvolumens, durch die Raumhöhe beschränkt, müssen Weitwinkelobjektive mit kleinen Brennweiten eingesetzt werden. Kleine Brennweiten führen allerdings zu großen radialen Linsenverzeichnungen wie in Abbildung 5.2, die durch geeignete Verfahren bei der Kamerakalibrierung (siehe Abschnitt 5.2.6) ausgeglichen werden müssen.

Die eingesetzen Kameras (vgl. Abbschnitt 2.1.7) verfügen in Kombination mit den verwendeten Objektiven über eine automatische Blendenregelung, die zusätzlich zu den Maßnahmen zur konstanten Beleuchtung für einheitliche Lichtstärken auf den nachfolgend beschriebenen CCD-Sensoren sorgt.

4.5  CCD-Sensoren

CCD-Sensoren sind ladungsgekoppelte Speicher (Charge-Coupled Device), welche aus einem dünnen, dotierten Silizium-Kristall bestehen, einfallendes Licht adsorbieren und aufgrund des Photoeffektes in elektrische Spannungen umwandeln. Die Bildinformation wird durch diesen in eine Matrix von analogen Spannungen umgewandelt, welche den jeweiligen Lichtintensitäten proportional sind. Die als Ladungsmuster gespeicherte Information wird nun zeilenweise ausgelesen und in ein elektrisches Videosignal umgewandelt. Das Videosignal entspricht der in Europa üblichen CCIR-Norm mit 625 Bildzeilen und 50 Bildern pro Sekunde, wobei ein Frame (Einzelbild) aus zwei jeweils aus um eine Zeile versetzte Halbbilder besteht, welche nacheinander übertragen werden.

Eine Alternative zu CCD-Sensoren sind Röhren-Video-Kameras, die aber heutzutage nur noch selten eingesetzt werden. Im Gegensatz zu Röhrenkameras haben CCD-Kameras folgende Vorteile:

• CCD-Kameras haben eine feste Geometrie, d.h. genauere Messungen sind möglich
• Kein Einbrennen der Bildinformation bei langen Belichtungszeiten
• geringere mechanische und elektrische (z.B. Störstrahlung) Unempfindlichkeit
• höhere Lebensdauer

Der in den verwendeten Kameras eingesetzte CCD-Sensor ist für den Schwarz-Weiß-Betrieb ausgelegt, d.h. er enthält nur eine CCD-Matrix für alle auftreffenden Lichtfarben. Farb-CCD-Sensoren bestehen im Prinzip aus drei Sensoren für jeden Bildpunkt, die mit Rot-, Grün- und Blaufiltern Versehen sind um so selektiv die Farbkomponenten des auftreffenden Lichts zu erfassen.

4.6   Framegrabber

Wesentlicher Bestandteil eines Bildverarbeitungssystems ist der sogenannte Framegrabber. Die Aufgabe des Framegrabbers ist es, das Videosignal zu digitalisieren, also in ein den Grauwerten³⁴ bzw. der Bildhelligkeit entsprechendes Bitmuster umzusetzen. In Framegrabbern wird das Videosignal, beispielsweise einer Kamera, zunächst gefiltert und verstärkt und einem ADC ³⁵ zugeführt. Meist wird für Grauwerte eine Auflösung von 8 Bit gewählt, was eine Differenzierung in 256 unterschiedliche Werte erlaubt. Eine Synchronisationsschaltung filtert die horizontalen und vertikalen Synchronsignale aus dem Video-Signal, und verwendet diese zur Steuerung des Framegrabbers. Das horizontale Synchronsignal HSYNC zeigt einen Zeilensprung, das vertikale VSYNC ein Halbbild³⁶- oder Vollbildwechsel an. Der Framegrabber verwendet diesen zeitlichen Rahmen um die digitalisierte Bildinformation synchron in seinen Videospeicher zu schreiben.

Die sogenannte Abtastrate bestimmt wieviele Pixel pro Bildzeile abgetastet werden. Die eingesetzten IC40-Framegrabberkarten unterstützen die Abtastfrequenzen 14,3 und 12,5 MHz, so daß für die Video-Normen CCIR-625 und EIA-525 quadratische Pixel erzeugt werden können. Solche quadratischen Pixel haben in der Bildverarbeitung den Vorteil, daß sich solche Bildinformationen für geometrische Berechnungen, beispielsweise von Objektumfängen oder Winkeln, besser eignen (Rechenzeitersparnis).[27]

Beispielhafte Berechnung der Pixelgeometrie für die CCIR-Norm:

CCIR-Norm:

Bei einem Pixeltakt von: P = 14,3×10⁶Pixel/s

Bei einem Seitenverhältnis von ²/₃ normierter Bildschirme und CCD-Sensoren sollte das Verhältnis von horizontalen zu vertikalen Pixeln ebenfalls
= [625/ 915,2] = 0,683 @ ²/₃ sein Þ Quadratische Pixel!

Die ,,Look Up Table'' LUT der IC40-Bildverarbeitungskarten stellt eine Transformationstabelle dar mit der eine schnelle Bildverarbeitung in Echtzeit möglich ist. Eine LUT ist im Prinzip ein sehr schneller Speicher mit 8 Adressleitungen und 8 Datenleitungen, also 256 Byte Speicher. Jedem 8-Bit Eingangswert kann also ein vorher definierter Ausgangswert zugewiesen werden. So können mit dieser Eingangs-LUT beliebige einstellige Operationen³⁷ oder Punkteoperationen auf das digitalisierte Grauwertbild, wie z.B. Gamma-Korrekturen oder Schwellwertoperationen, angewendet werden. Im übrigen verfügen die IC-40-Karten ebenfalls über eine Ausgangs-LUT durch die der Videoausgang der Karten in der Lage ist ein farbiges Videosignal zu generieren. Hier repräsentiert die LUT die Farbtabelle des Systems, d.h. bis zu 256 Farben können gleichzeitig dargestellt werden. Jedem 8-Bit-Wert des Videospeichers wir eine von 256 Farben zugeordnet.

4.7   Kantenextraktion

Die nachfolgende Stufe des beschriebenen Bildverarbeitungssystems ist die Kantenextraktion. Hier soll zunächst auf allgemeine Verfahren eingegangen werden, die sich mit Hilfe von Filteroperationen im Ortsbereich ausführen lassen. Man unterscheidet diese Filterverfahren in lineare- und nichtlineare Filter. Lineare Filter auch als nichtrekursive Filter, und in angelsächsischem Sprachraum als ,,finite impulse response'' FIR bezeichnet, haben den Vorteil, daß aufgrund des Überlagerungsprinzips, ihre Antwort auf beliebige Signale bestimmt werden kann, wenn die Antwort des Operators auf einen idealen Impuls (Impulsantwort) bekannt ist. Sie können aus diesem Grund einfach in schnellen Hardware-Bausteinen mit LUT's realisiert werden. Durch lineare Filter können aber im wesentlichen nur Tiefpaß-, Hochpaß- und Bandpaßfilter realisiert werden, während mächtigere Operatoren, wie beispielsweise der im folgenden erläuterte Sobel-Operator rekursiver, nichtlinearer Natur sind.

4.7.1  Lineare Filter

Lineare Filter unterscheidet man wiederum in eindimensionale- und zweidimensionale lineare Filter. Ihre Funktionsweise läßt sich mit folgender Handlungsanweisung erläutern. Die Grauwerte der umgebender Pixel und eines betrachteten Pixels werden mit Gewichtungskoeffizienten multipliziert, aufsummiert und ergeben so den neuen Grauwert des betrachteten Pixels. Wenn die umgebenden Pixel in einer Linie liegen, beizeichnet man diese linearen Filter als eindimensional, wenn die Filteroperation auf eine meist quadratische zweidimensionale Umgebung eines Pixels angewandt wird, als zweidimensional. Die Summation erfolgt in diesem Fall über zwei Indizes:

Der Grauwert f_jk des Bildpunktes an der Stelle (j,k) wird unter Verwendung der Matrix der Gewichtskoeffizienten h_mnin in den Grauwert g_jk überführt. Die Anzahl der berücksichtigten Nachbarpunkte wird durch die Indizes p und q festgelegt. Häufig werden 3x3 Matrizen verwendet, in diesem Fall ist p = q = 1 .[27]

Beispiel für o.g. linearen Filter ist der Gauß'sche Tiefpaß:

Die Division durch 16 ist notwendig, weil die Matrix 4.2 nicht normiert ist. Die Summe der Koeffizienten der Matrix muß den Wert 1 haben, um eine generelle Aufhellung bzw. Abdunkelung aller Pixel des Bildes zu verhindern. Ein solcher Tiefpaßfilter führt zu einer Entfernung von hochfrequenten Störungen, aber auch zu einer ,,Weichzeichnung'', d.h. einer Abschwächung hochfrequenter Kanten.

Lineare Filter die Hochpaßeigenschaften besitzen und daher gut für eine Kantenhervorhebung geeignet sind, haben folgende Struktur:

Durch die Wahl der Koeffizienten h_mn werden Vorzugsrichtungen festgelegt. Mathematisch entsprechen diese Hochpaßfilter einer numerischen Ableitung in der diskreten Ebene und werden daher als Gradienten bezeichnet. Der Filter 4.4 wird seiner Vorzugsrichtung nach als Nordgradient, der Filter 4.5 als Südgradient bezeichnet. Die durch die negativen Koeffizienten der Matrix auftretenden negativen Grauwerte können durch eine Verschiebung des Nullpunktes auf 127 und eine Begrenzung der Extremwerte auf 0 und 255 verhindert werden.

*0.45!

*0.45!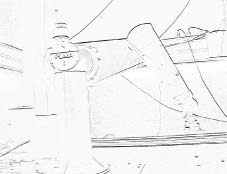

Ein linearer Filter ohne Vorzugsrichtung ist der Laplace-Filter. Er ist für kontinuierliche Funktionen definiert durch:

Ein entsprechender Laplace-Filter in der diskreten Ebene hat dann folgende Struktur:

4.7.2  Nichtlineare Filter

Noch besser geeignet für Kantenextraktionsverfahren sind nichtlineare Filter, wie zum Beispiel die Roberts-, Kirsch-, und Sobel-Operatoren. Der Sobel-Operator soll hier beispielhaft erläutert werden. Er ist als Absolutbetrag des Gradientenvektors, der sich aus den Ableitungen in X- und Y-Richtung ergibt, definiert. Durch übertragungen in die diskrete Ebene ergibt sich:

oder näherungsweise

mit

Mit diesem Verfahren kann eine Kantenverstärkung weitgehend unabhängig von Beleuchtungsinhomogenitäten durchgeführt werden.

4.7.3  Realisierung der Kantenverstärkung auf den verwendeten THINEDGE-Bildverarbeitungskarten

Die Realisierung der Kantenverstärkung erfolgt auf den THINEDGE-Karten hardwaremäßig in vier Schritten:

1. Richtungsorientierte FIR-Filter finden die Kanten in horizontaler und vertikaler Richtung.
2. Die Größe und Richtung der lokalen Gradienten wird mittels Hilfe der arithmetischen look-up-tables berechnet.
3. Extraktion der Gradienten-Maxima und Transformation zu binären Kontur Werten.
4. Richtungskontrollierte Ausdünnung der Konturen auf die Breite von einem Pixel.

Die Punkte 1 bis 3 der beschriebenen Funktionalität können durch lineare Filteroperationen realisiert werden. Die richtungskontrollierte Ausdünnung der Konturen erfordert allerdings nichtlineare und irreversible Verfahren. Diese Verfahren werden als Skelettierung oder Verdünnung bezeichnet und können vollständig unter Verwendung von look-up-tables in Hardware realisiert werden. Ein genaue Beschreibung dieser Verdünnungsalgorithmen findet sich in [27]. Eine Ausdünnung der Kantenkonturen erleichtert die Vektorisierung von Linienelementen, wie sie im folgenden Abschnitt 4.8 erläutert wird. Details zur Hardware-Realisierung finden sich in [10].

4.8   Vektorisierung

Um für die Weiterverarbeitung eine numerisch vorliegende Kontur zu gewinnen, können aus den ausgedünnten Pixelbildern sogenannte Konturketten gebildet werden. Diese Pixelkonturen werden zur Speicherplatzersparnis in einem sogenannten Kettencode abgelegt, d.h. nur die Koordinaten des Anfangs- und Endpunktes werden gespeichert. Für die Zwischenpixel wird jeweils ein Wert für die Richtung relativ zum letzten Pixel gespeichert.

Eine wesentlich elegantere, aber aufwendigere Methode ist die Vektorisierung der Konturen, bei der die Konturen durch gerade Linien angenähert werden. Vorteil einer Darstellung im Vektorformat ist beispielsweise die einfache Weiterverarbeitung und die Unempfindlichkeit vektorieller Daten gegenüber einer Skalierung.

4.8.1   Realisation der Vektorisierung auf den verwendeten VECTOR-Bildverarbeitungskarten

Der Vektorprozessor approximiert jede Kontur mit als Vektoren bezeichneten geraden Linien. Wenn die Differenz der lokalen Orientierung zwischen angrenzenden Pixeln kleiner ist, als ein spezifizierter Winkel, wird die Gruppe von Pixeln in einen Vektor konvertiert. Der spezifizierte Winkel, welcher im Bereich von 1,4 bis 21 Grad variiert werden kann, wird in einem programmierbaren Register gespeichert. Ein zusätzlicher spezieller ,,thinmode'' teilt Linien in Vektoren von 1 bis 1,4 Pixeln Länge, um eine höchstmögliche Genauigkeit zu erreichen. Die Approximationsparameter kontrollieren den Datenreduktionsfaktor, der abhängig von der beobachteten Szene zwischen 50 und 5000 liegen kann, und sollten daher dem Problem angemessen angepaßt werden.

Die Vektorisierungs-Hardware arbeitet in zwei Stufen. Die erste Stufe führt die Hauptaufgaben, wie die Konturdetektion, das Markieren von Konturpunkten und den Winkelvergleich durch. Ein Zähler generiert die Konturnummern mit einer Kapazität von bis zu 64K Kontur-Elementen für einen Frame. Die Konturpunkte werden durch eine 2-D-Maske klassifiziert, welche die aktuell bearbeiteten Pixel und ihre jeweiligen Nachbarn enthält. Die Erkennung der Nachbarschaft arbeitet im Uhrzeigersinn. Ein programmierbarer Komparator vergleicht die lokale Kantenorientierung mit der Orientierung des momentan bearbeiteten Vektors, so daß der Vektorisierer lokale und globale Orientierungen zur Vektorisierung eines Bildes verwendet.

Die zweite Stufe detektiert Beziehungen zwischen Nachbarkonturen und generiert Verbindungsinformationen zwischen zwei verbundenen Einzelkonturen. Um die Synchronität dieser Verarbeitungsstufen zu wahren, arbeiten die VECTOR-Karten mit mehreren FIFO³⁸-Linebuffern. Die Größe dieser Linebuffer begrenzt die Anzahl der verarbeitbaren Pixel pro Zeile. Die Standardausführung der VECTOR-Bildverarbeitungskarten ist mit 1kByte großen FIFO's ausgestattet, es ist allerdings leicht möglich diese FIFO's gegen größere, bis maximal 16kByte Größe auszutauschen. Der gesamte Vektorprozessor ist mittels programmierbarer Gate-Arrays (LCA's) realisiert worden. Die Operationsprogramme der LCA's sind in zwei SPROM-Bausteinen abgespeichert und werden nach dem Einschalten oder nach einem System-Reset automatisch eingelesen.

Ausgabestufe des Vektorisierers ist ein Symbol-Buffer von 2K-Wörtern³⁹, jeder Eintrag kann 74Bit umfassen. die Konturbeschreibung von mehreren Frames wird in der Reihenfolge ihrer Verarbeitung abgespeichert.

Jeder Eintrag enthält:

• Konturnummer
• Start/Ende-Flag der Kontur
• Nachbarkonturnummer
• Start/Ende-Flag der Nachbarkontur
• Absolute X-Y-Koordinaten des Vektors
• Lokale Orientierung

Zusätzlich wird der Buffer- und Vektorisierungsstatus in den Symbolbuffer eingeblendet. Der Symbolbufferzugriff (read-only) ist über den VME- und VSB-BUS nur im Longword-Modus möglich⁴⁰.

4.9   2-D-Objekt-Segmentierung

Der nun folgende Schritt der Bildverarbeitung beschäftigt sich damit, geschlossene 2-D-Konturen zu finden, um auf diese Weise 2-D-Objekte zu segmentieren. Dieser Verarbeitungsschritt ist der Erste, der rein softwaretechnisch realisiert wurde. Der durch die Hardware-Vektorisierung stark reduzierte Datenstrom muß nun in Echtzeit verarbeitet werden. Erst diese starke Reduzierung in Hardware macht eine Echtzeitverarbeitung mit Prozessoren der Motorola 68K-Klasse möglich.

Um die vorhandene Rechenleistung gut auszunutzen, wurden die CPU's der IC40-Bildverarbeitungskarten ausgewählt, diese Aufgabe zu übernehmen. Da für jeden der beiden CCD-Sensoren eine eigene Framegrabber-Karte mit integrierter CPU eingesetzt wird, bietet sich in dieser Konfiguration die Gelegenheit, die 2-D-Verarbeitung auch softwareseitig zu parallelisieren.

Die VECTOR-Karten führen, wie im Abschnitt 4.8.1 beschrieben, in einer zweiten Verarbeitungsstufe eine einfache Suche nach Nachbarkonturen durch. Diese Konturen werden über Verweise zu einer Konturkette verbunden. Praktische Untersuchungen ergaben, daß auch geschlossene Konturen nicht vollständig von der Hardware-Vektorisierung zu einer Kette zusammengeschlossen werden. Beobachtete reale Objekte enthalten aufgrund von Störungen durch Beleuchtungseinflüsse (Schattenverläufe, Reflexe) meist kleine Lücken in den Konturverläufen. Die Aufgabe der 2-D-Software-Module auf den IC40-Karten ist es, diese Lücken zu schließen und mit geeigneten Verfahren geschlossene Konturen, im folgenden 2-D-Objekte genannt, zu detektieren.

Dazu werden folgende vereinfachende Annahmen getroffen:

• Die zu erkennenden Konturen befinden sich entweder vollständig innerhalb des Frames, oder ihre Fläche ist kleiner als die Hälfte des Frames.
• Für den Einsatz der Bildverarbeitung für die Kollisionsvermeidung ist weniger die genaue Kontur, sondern die Lage der Extremwerte einer Kontur entscheidend.

Der realisierte Algorithmus bearbeitet die in Abschnitt 4.8.1 erläuterte Ausgabedatenstruktur der VECTOR-Karten auf folgende Weise:

• Für jedes Kontursegment werden alle anderen Kontursegmente auf mögliche Nachbarschaft untersucht.
• Jedem Kontursegment werden bis zu zwei Nachbarkonturen zugeordnet. An jedem Ende der Kontur kann eine Nachbarkontur detektiert werden, wenn ein Kontursegment existiert, dessen Abstand zur untersuchten Kontur kleiner ist als ein Schwellwert Delta. Dieser Schwellwert wird heuristisch so gewählt, daß für die aktuellen Beleuchtungsbedingungen entstehende Lücken in Konturketten sicher geschlossen werden können.
• Nun wird für jedes Konturelement eine Konturkette gebildet, indem an einer Seite Nachbarkonturen hinzugefügt werden bis entweder kein Nachbar mehr gefunden werden kann (Konturende), der Vorrat an Konturelementen erschöpft istoder ein Element der Konturkette auf das Anfangselement verweist.
• In den Fällen, in denen kein Nachbar mehr gefunden werden kann oder die Konturelemente erschöpft sind, wird mit dem nächsten Kontursegment fortgefahren.
• Im letzteren Fall ist eine geschlossene Kontur erfolgreich erkannt worden und ihre Elemente werden gekennzeichnet damit die gleiche Konturkette nicht mehrfach gefunden wird.
• Die Extremwerte der erkannten Konturkette werden ermittelt und in einer Datenstruktur abgespeichert.
• Wenn alle Konturelemente abgearbeitet worden sind, wird die Anzahl der erkannten geschlossenen Konturketten abgespeichert.

Dieser einfache und schnelle Algorithmus ist in der Lage Konturketten in Echtzeit, also für 25 Frames pro Sekunde zu erkennen, und ihre Extremwerte für eine weitere Bearbeitung zur Verfügung zu stellen. Er führt eine weitere Datenreduktion durch, aus den bis zu 4kByte Konturdaten werden die X- und Y-Extremwerte von bis zu 20 2-D-Objekten⁴¹ .

Die lokale Software auf den IC40-Bildverarbeitungskarten übernimmt außerdem die Initialisierungsprozeduren, die für den ordnungsgemäßen Betrieb der VECTOR-Karten notwendig sind.

Darüberhinaus ist die lokale Software Kommunikationspartner der Haupt-CPU des Bildverarbeitungssystems und muß die Kommunikationsprotokolle der beiden realisierten Kommunikationsverfahren einhalten.

4.10   Kommunikation der Bildverarbeitungskomponenten

Für eine weitergehende Stereo-3-D-Bildverarbeitung ist eine Zusammenführung der Informationsströme der beiden 2-D-Bildverarbeitungskanäle notwendig. Die Haupt-CPU-Karte kommuniziert mit beiden IC40-Bildverarbeitungskarten über zwei mögliche Kommunikationswege.

• Direkter Zugriff in den Adressbereich der IC40-Bildverarbeitungskarten über den VME-BUS. Die Haupt-CPU-Karte ist der VME-BUS-Master, d. h. Zugriffe vom VME-Bus aus auf das lokale RAM der IC40-Karten haben Priorität vor Speicherzugriffen der Onboard-CPU. Die lokale IC40-CPU wird während eines Zugriffs auf ihr RAM vom VME-BUS aus angehalten. Im lokalen RAM der IC40 definiert die entwickelte Software einen Kommunikationsbereich, der die in Abschnitt 4.9 erläuterte 2-D-Bildinformation in einer Datenstruktur gekapselt enthält. Dieser Kommunikationsbereich muß in einem Bereich liegen, auf den die lokale CPU ohne Umweg über den Speicher-Cache zugreifen kann, da der Cache-Controller keine Möglichkeit hat zu erkennen, ob eventuell Daten in dem betreffenden Speicherbereich von einem anderen Prozessor geändert wurden. Außerdem ist eine geeignete Synchronisation vorgesehen, um zu verhindern, daß die Haupt-CPU ungültige oder noch nicht vollständig geschriebene Daten einliest.
• Kommunikation über die IC40-Device-Treiber des OS9-Betriebssystems auf der Haupt-CPU. Zum Lieferumfang der IC40-Bildverarbeitungskarten gehört ein OS9-Devicetreiber, der sich, wie im Abschnitt 2.2.2.1 beschrieben, dazu eignet, die Standardein- und ausgabe der IC40-Karten von der Haupt-CPU-Karte aus zu bedienen. Diese Device-Schnittstelle wird in diesem zweiten Ansatz dazu genutzt ein einfaches Kommunikationsprotokoll abzuwickeln. Hierfür schreibt die anfordernde, auf der Haupt-CPU-Karte ablaufende Software einen Anforderungsstring in das IC40-Device, während die lokale IC40-Software auf diesen String auf ihrem Standart-Input-Device wartet, um ihrerseits mit einem Datenpaket auf ihrer Standardausgabe zu antworten. Ein wesentlicher Vorteil dieser Art der Kommunikation ist, daß sie gepuffert stattfindet, d.h. keine der beteiligten Kommunikationspartner muß umgehend auf ein Datenpaket antworten. Außerdem verhindert die Art der Implementierung des Protokolls, daß bei beiden Kommunikationspartnern Polling auftritt. Die IC-40-Karten fahren einfach mit der Bearbeitung der nächsten Frames fort, wenn keine Anforderung auftritt. Die Haupt-CPU setzt jeweils einen neuen Request ab, wenn sie ein Datenpaket erfolgreich gelesen hat. Sind noch nicht genügend Bytes für ein Datenpaket im Puffer, wird die entsprechende Bildverarbeitungskarte für einen Verarbeitungszyklus ignoriert, und mit der Verarbeitung der anderen Datenquellen fortgefahren.

Das erste beschriebene Verfahren führt zu häufigen VME-BUS-Zugriffen der Haupt-CPU auf das RAM der IC40-CPU's. Da die lokalen IC40-CPU's jeweils während eines solchen Vorgangs angehalten werden, bzw. selber nicht über den VME-BUS auf die VECTOR-Karten zugreifen können, kommt es bei diesem Verfahren zu Timing-Problemen mit den VECTOR-Karten. Aus diesem Grund wurde das zweite Verfahren für die Kommunikation mit den IC40-Karten ausgewählt.

4.10.1  Initialisierung der Bildverarbeitungskarten

Vor ihrer Verwendung⁴² müssen alle Bildverarbeitungskarten initialisiert werden. Diese Initialisierung betrifft im Falle der IC40-Karten die lokale CPU, das lokale Betriebssystem und die Register der Framegrabber. Die notwendigen Befehle zum Download des lokalen Betriebssystems der IC40-Karten sind im Abschnitt 2.2.2.1 erläutert. Die THINEDGE-Karten werden durch das Programm THININI initialisiert, welches als Binary und im Quellcode zum Lieferumfang der Bildverarbeitungskarten gehört. Die THINEDGE-Karten sind leider von den IC-40-CPU's nicht direkt adressierbar, weshalb die erste Initialisierung von der Haupt-CPU aus gestartet werden muß. Die ebenfalls im Quellcode vorliegende Initialisierungsroutine VECTINI für die VECTOR-Karten wurde so modifiziert, daß sie auf den IC-40-CPU's ablauffähig ist und alle in den Abschnitten 4.9 und 4.10 beschriebenen Funktionalitäten enthält.

Die komplette Initialisierung des System wurde zu einem einzigen OS9-Shellscript zusammengefaßt, welches der Benutzer unter dem Namen
START_ALL aufrufen kann. Dieses Shell-Script ist im Anhang auf Seite pageref aufgeführt.

4.10.2   Datenfluß (VME-BUS, VideoBUS) und Datenreduktion durch Bildverarbeitung

Zusammenfassend kann der Datenfluß im Bildverarbeitungssystem folgendermaßen charakterisiert werden:

• Die beiden Videosignale werden über die Videoeingänge der IC40-Karten dem Bildverarbeitungssystem zugeführt. Das Schwarz/Weiß -Videosignal hat in etwa eine Bandbreite von 14,3 MHz was in etwa einer Datenrate von 14.3 MByte/Sekunde entsprechen würde, wenn jeder Pixel eine Auflösung von 8 Bit für seine Intensität besäße. Ein analoges Signal enthält kontinuierliche und keine diskreten Grauwerte, so daß läßt sich die enthaltene rohe Informationsmenge nur abschätzen läßt, sie ist allerdings um ein mehrfaches größer, als die eines mit 8 Bit digitalisierten Signals.
• Dort werden die Bilder digitalisiert und über den Videobus an die THINEDGE-Karten weitergegeben. Die digitalisierten Bilder, mit einer Größe von 768x576 Punkten, einer Grauwerttiefe von 8 Bit und einer Framerate von 25, beinhalten einen Datenstrom von 10,8 MByte/s.
• Die THINEDGE-Karten reduzieren die Bildinformationen auf eine Bitmap mit einer Bit-Grauwerttiefe, also auf ein Bild welches ausschließlich aus schwarzen und weißen Bildpunkten besteht. Die Datenreduktion ist in dieser Stufe also eine um den Faktor 8. Der verbleibende Datenstrom von 10,8 MBit/s wird jeweils über den VideoBUS an die VECTOR-Karten weitergereicht.
• Die VECTOR-Karten vektorisieren die ausgedünnten Konturen zu Linienelementen, die bis zu 4KByte Speicher pro Frame belegen, also eine Datenrate von 100KByte/s generieren. Über den VME-BUS werden diese Daten von den IC40-Bildverarbeitungskarten ausgelesen und dort weiter zu Konturketten verarbeitet.
• Die Software auf den IC40-Karten erzeugt bis zu 20 geschlossene Konturzüge aus den Vektoren und berechnet für diese je vier Extremwerte. (Datenstrom bei Speicherung in Integerwerten: 160 Bytes/s, durch den Protokolloverhead ca. 30% größerer Datenstrom)
• Die beiden 2-D-Datenströme werden nun von der Haupt-CPU über den VME-BUS gelesen und zu einem 3-D-Datenstrom umgerechnet, welcher nun die Extremwerte von bis zu 20 3-D-Objekten enthält. Aus 2x 4000 Bytes/s werden so 240 Bytes*25Frames = 6000 Bytes/s

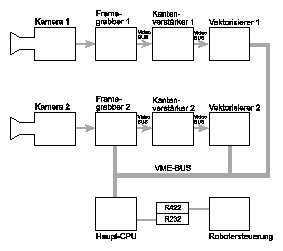
So wird also im Zuge der Bildverarbeitung ein Datenstrom von ca. 2x 30 MByte/s auf eine Informationsmenge von 6000 Bytes/s reduziert. Es handelt sich damit um eine Datenreduktion um etwa vier Zehnerpotenzen.

Die Qualität der Information nimmt allerdings während des Bildverarbeitungsprozesses kontinuierlich zu, während zunächst ein großer roher Datenstrom vorliegt, ist der Datenstrom am Ende auf die für das Problem relevante Information reduziert.

Kapitel 5
3-D-Bildverarbeitung

Um den in Abschnitt 4.10.2 erwähnten Übergang von 2-D auf 3-D-Informationsverarbeitung zu vollziehen, ist es notwendig, auf die Grundlagen der Stereobildverarbeitung einzugehen.

Die Methoden zur Gewinnung von 3-D-Bildinformationen können in aktive und passive Verfahren unterschieden werden. Bei den aktiven Methoden werden die zu untersuchenden Szenen mit gepulstem oder strukturiertem Licht⁴³ beleuchtet. Die räumliche Information kann dann aus verschiedenen physikalischen Größen, wie Laufzeiten, geometrischen Verzerrungen und Interferenzstrukturen bestimmt werden. Zu diesen Verfahren zählen die optische Flugzeitmessung (Lidar), die Triangulation mit Lichtpunktprojektoren, die Lichtschnittechnik und die interferometrische Längenmessung [27].

Das hier eingesetzte Verfahren gehört zu den passiven Verfahren, die mit zwei oder mehreren Kameras (Stereobildverarbeitung) oder mit einer einzigen Kamera (monokulare Bildverarbeitung) arbeiten.

5.1  Stereobildverarbeitung für Industrieroboter

Für den Einsatz von Bildverarbeitung für Industrieroboter und mobile Systeme, ist je nach Aufgabenstellung ein Verwendung von raumfesten oder mitbewegten Kameras sinnvoll. Beispielsweise bietet sich für die bildverarbeitungsgestützte Roboterkalibrierung ein mitbewegtes Kamerasystem an. Dieses Verfahren stellt gewissermaßen die Umkehrung des hier beschriebenen Verfahrens dar. Ein an die Roboterhand montiertes geeichtes Kamerasystem wird eingesetzt um mittels eines Eichkörpers einen Roboter zu kalibrieren[14]. Für mobile Systeme ist eine Gewinnung von Stereo-Informationen auch mit Ein-Kamera-Systemen möglich, wenn zeitliche Veränderungen der Bildinformation ( Optischer Fluß⁴⁴) bei Betrachtung ortsfester starrer Umgebungspunkte durch Eigenbewegung oder Bewegung der Kamera ( Active Vision) erzwungen werden.

Für die bildverarbeitungsgestützte Kollisionsvermeidung ist die Arbeitsraumüberwachung eines Industrieroboters am besten durch raumfester Kameras zu gewährleisten. Passive Verfahren mit Einsatz von zwei oder mehreren Kameras eignen sich besonders für dieses Verwendungsgebiet. Prinzipiell ist mit dem beschriebenen passiver Verfahren eine 3-D-Informationsgewinnung mit zwei Kameras möglich, allerdings können zur Vermeidung von Phantombereichen auch mehrere Kameras genutzt werden. Phantombereiche sind Bereiche des Überwachungsraumes, die nicht durch eine Kamera eingesehen werden können. Bereiche die nicht durch zwei Kameras gleichzeitig eingesehen werden, sind für eine Stereobildverarbeitung mit dem eingesetzten Verfahren nicht zu überwachen. Solche Phantombereiche lassen sich nie ganz vermeiden, wenn komplizierte Objekte mit konvexer Gestalt beobachtet werden. Außerdem sind bestimmte Kameraanordnungen günstig für eine Auflösung der Korrespondenz zweier 2-D-Bildpunkte im dreidimensionalen Raum. Stereobildverarbeitung gewinnt räumliche Informationen aus der Disparität⁴⁵ korrespondierender Punkte und ist daher im wesentlichen auf die Korrespondenzauflösung angewiesen.

Im beschriebenen Aufbau werden zwei Kameras eingesetzt, die an einem Träger oberhalb der Roboterarbeitszelle in einer Ebene orientiert angebracht sind. Der Abstand der Kameras bzw. ihre Brennweite sind so gewählt worden, daß der gesamte Arbeitsraum überwacht werden kann. Durch Hindernisse verursachte Phantombereiche sind für die hier beschriebene Implementierung durch den Einsatz eines Fuzzy-Logic basierten Kollisionsvermeidungsalgorithmus (siehe Abschnitt 7) relativ unkritisch. Phantombereiche, die durch den Industrieroboter selbst entstehen sind insofern unkritisch, weil ein Hindernisobjekt, das sich dem Roboter nähert sofort zu einer Ausweichbewegung führt. Kann die Ausweichbewegung nicht schnell genug ausgeführt werden oder hat der Roboter keine Möglichkeit mehr auszuweichen, wird er gestoppt. Der Roboter selber ist nicht Gegenstand der 3-D-Sensorüberwachung, da seine Ist-Position dem Bildverarbeitungssystem kontinuierlich von der Robotersteuerung mitgeteilt wird.

Die Kameras eines Stereobildverarbeitungssystems müssen vor ihrem Einsatz kalibriert werden. Die folgenden Abschnitte beschäftigen sich daher mit den Grundlagen und der Vorgehensweise bei der Kamerakalibrierung.

5.2  Das Kameramodell

Voraussetzung für die Kamerakalibrierung ist ein mathematisches Kameramodell. Im ersten Ansatz wird hier von einer einfachen Lochkamera ausgegangen. Eventuelle Linsenverzeichnungen werden später durch geeignete Korrekturfaktoren berücksichtigt. Eine Lochkamera bildet Punkte einer beobachteten Umgebung, hier vereinfacht als Arbeitsvolumen mit zugeordnetem Welt-Koordinatensystem dargestellt, auf einer Sensorfläche ab. Die z-Achse des Weltkoordinatensystems ist zweckmäßigerweise so orientiert, daß sie mit der z-Achse des Arbeitsvolumens zusammenfällt. Das Weltkoordinatensystem ist ein kartesisches Koordinatensystem mit den Dimensionen x,y und z . Das Sensorkoordinatensystem wir durch die Dimensionen u und v gekennzeichnet (siehe Abbildung 5.1)

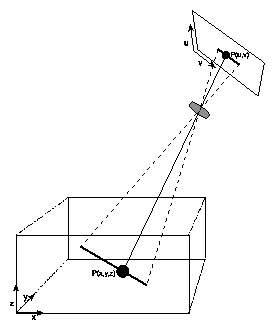
Ein Punkt im Raum mit den Koordinaten P_x,P_y und P_z wird abgebildet in die Sensorebene als P_u und P_v .

5.2.1   Homogene Koordinaten

Solche Koordinatentransformationen lassen sich sehr gut mit homogenen Koordinaten beschreiben.

Homogene Koordinaten eignen sich zur einheitlichen Beschreibung von geometrischen Transformationen durch Matrixmultiplikationen. Transformationen und die Gesamtskalierung werden in einer 4×4 Transformationsmatrix zusammengefaßt. Diese Transformationsmatrix enthält die Komponenten:

Vorteile⁴⁶ dieser Darstellung sind die einheitliche Behandlung aller Transformationen und die Möglichkeit komplexe Transformationen als Matrixmultiplikationen durchzuführen. Mehrere Transformationen (z.B. Translation und Rotation) müssen nicht mehr nacheinander ausgeführt werden, sondern es wird einmalig die Gesamttransformationsmatrix berechnet, mit der dann die homogenen Koordinaten der zu transformierenden Punkte multipliziert wird. Außerdem lassen sich diese Transformationen einfach durch Matrixinversion umkehren.

Der Übergang von kartesischen Koordinaten zu homogenen Koordinaten gestaltet sich folgendermaßen:

Kartesische Koordinaten eines Punktes im Raum:

Entsprechende homogene Koordinaten:

Die möglichen Transformationen mit homogenen Koordinaten sind in Tabelle 5.1 aufgeführt.

Transformation	Transformationsmatrix für homogene Koordinaten
Translation	(	1 0 0 -Tx 0 1 0 -Ty 0 0 1 -Zz 0 0 0 1	) ·(	x y z 1	) ® (	x¢ y¢ z¢ 1	)
Rotation um die x-Achse	(	1 0 0 0 0 cos(ax) sin(ax) 0 0 -sin(ax) cos(ax) 0 0 0 0 1	) ·(	x y z 1	) ® (	x¢ y¢ z¢ 1	)
Rotation um die y-Achse	(	cos(ay) 0 -sin(ay) 0 0 1 0 0 sin(ay) 0 cos(ay) 0 0 0 0 1	) ·(	x y z 1	) ® (	x¢ y¢ z¢ 1	)
Rotation um die z-Achse	(	cos(az) sin(az) 0 0 -sin(az) cos(az) 0 0 0 0 1 0 0 0 0 1	) ·(	x y z 1	) ® (	x¢ y¢ z¢ 1	)
3-D-Skalierung mit Faktoren Sx,Sy,Sz
	(	Sx 0 0 0 0 Sy 0 0 0 0 Sz 0 0 0 0 1	) ·(	x y z 1	) ® (	Sx·x Sy·y Sz·z 1	)
Gesamtskalierung Sg	(	1 0 0 0 0 1 0 0 0 0 1 0 0 0 0 1/Sg	) ·(	x y z 1	) ® (	x y z 1/Sg	)

Die Translations- und Rotationstransformationen lassen sich auch als 3×3 Matrizen beschreiben wie z.B. die Rotation um die x-Achse:

Es ist leicht zu erkennen, das diese Matrix für eine Darstellung in homogenen Koordinaten nur einfach erweitert wird. Die 3×3 Matrizen sind ein Spezialfall der allgemeineren 4×4 Matrizen.

5.2.2  Physikalisches Kameramodell

Klassische Verfahren[16] der Kamerakalibrierung verwenden ein physikalisches Kameramodell, das 11 verschiedene Parameter zur Beschreibung einer Kamera benötigt, welche in interne und externe unterschieden werden (siehe Tabelle 5.2).

Neuere Ansätze[19] erweitern dieses Modell noch um zwei weitere Parameter, welche eine zusätzliche Bildebenenverkippung berücksichtigt. Die notwendigen Schritte um in diesem Modell aus 3-D-Weltkoordinaten
( X_w,Y_w,Z_w) geräteabhängige 2-D-Bildkoordinaten zu gewinnen sind folgende:

1. Schritt: Transformation der Translation und Rotation Þ 3-D-Kamerakoordinaten
2. Schritt: Perspektivprojektion mit B Þ Ideal unverzerrte Bildkoordinaten
3. Schritt: Radiale Linsenverzerrung mit k₁ und k₂ Þ Verzerrte Bildkoordinaten
4. Schritt: Fehler im Ursprung und Skalierungsfaktoren s_x und s_y Þ geräteabhängige Bildkoordinaten [15]

Mit geeigneten Kalibrierungsverfahren können die internen Kameraparameter bestimmt bzw. die externen Parameter vermessen werden.

5.2.3  Einfaches mathematisches Kameramodell mit homogenen Koordinaten

Wenn aber die Bestimmung der Kameraparameter nicht das primäre Ziel der Kalibrierung ist, sondern nur eine Transformation von 3-D-Weltkoordinaten in ein 2-D-Sensorkoordinatensystem gewünscht wird, ist die Wahl einer 4×4 Transformationsmatrix als mathematisches Kameramodell sinnvoll. Alle in Abschnitt 1 genannten Transformationsschritte lassen sich, bis auf die nichtlineare Linsenverzeichnung,⁴⁷ in einer einzigen Transformationsmatrix darstellen, die im folgenden als Kameramatrix bezeichnet wird.

Die Kameramatrix M transformiert 3-D-Weltkoordinaten ( x,y,z) in 2-D-Bildkoordinaten (u,v) :

bzw.

Die Elemente a₁₁ bis a₄₄ sind noch unbekannt, aber eine geeignete Wahl dieser Koeffizienten repräsentiert jede mögliche lineare Transformation der ( x,y,z) - in (u,v) -Koordinaten (die Koordinate w wird für eine Transformation in eine Ebene nicht genutzt). Gelingt es die Koeffizienten der Kameramatrix zu bestimmen, sind die (u,v) -Koordinaten errechenbar. Umgekehrt ist eine Transformation von (u,v) nach ( x,y,z) nur möglich, wenn eine zusätzliche Information zu Verfügung steht (2 Gleichungen, 3 Unbekannte). Die zusätzliche Information wird bei der Stereobildverarbeitung aus einer zweiten Kameramatrix gewonnen ( (u₂,v₂) , also 4 Gleichungen mit 3 Unbekannten).

Da die Koordinate w im 2-D-Bild nicht benötigt wird und homogene Koordinaten explizit einen Skalierungsfaktor beinhalten (jede konstante Multiplikation dieser Matrix repräsentiert die gleiche Transformation), kann die Gleichung 5.4 folgendermaßen vereinfacht werden:

löst man nun nach u und v auf, erhält man:

und

Weil die Koordinate w in Ausdruck 5.6 für Transformationen auf ein 2-D-Bild nicht benötigt wird, stellt man die Kameramatrix M häufig als 3×4 Matrix dar.

5.2.4   Die Kamerakalibrierung

Jede bekannte Welt-Bild-Korrespondenz impliziert nun zwei Gleichungen mit 11 Unbekannten. Wenn also mindestens 6 Korrespondenzen von ( x,y,z) -Koordinaten zu (u,v) -Koordinaten bekannt sind, lassen sich alle 11 Elemente a_ij bestimmen. Dieses Verfahren ist erstmals in [17] beschrieben und eignet sich sehr gut für eine einfache und robuste Kamerakalibrierung.

Schreibt man die Unbekannten a_ij in Form eines 11-Tupels:

Ausdruck 5.9 ist eine Schar linearer Gleichungen der Form

wobei A die oben konstruierte 2n ×11 Matrix, B ein 11-Tupel mit 11 Unbekannten und C ein 2n -Tupel repräsentiert.

M bzw. alle Elemente von M können also mit Hilfe der Methode der kleinsten Quadrate (siehe [24]) bestimmt werden, wenn 6 oder mehr⁴⁸ linear unabhängige Korrespondenzen bekannt sind.

5.2.5  Vorteile des Verfahrens von Bolles, Kremers und Cain [17]

Die beschriebene Kamerakalibrierung hat den Vorteil, das weder interne noch externe Kameraparameter bekannt sein müssen. Die Orientierung der Kameras muß nicht bekannt sein oder vermessen werden. Durch die Verwendung von homogenen Koordinaten ist die Anzahl der notwendigen Transformationen auf eine einzige beschränkt, was sich positiv auf die notwendige Rechenzeit für eine Implementierung dieser Algorithmen auswirkt. Der einzige Nachteil dieses Verfahrens, nämlich die fehlende Möglichkeit interne- und externe Kameraparameter zu berechnen, wird relativiert durch Untersuchungen von Ganapathy [21], in denen eine Dekompositionstechnik vorgestellt wird, die es erlaubt alle nötigen internen- und externen Kameraparameter aus der Kameramatrix M zu berechnen. Dieses Dekompositionsverfahren wurde von Faugeras und Toscani [22] auf die Bestimmung von epipolaren Kamerageometrien, und von Puget und Skordas [23] für die Kalibrierung einer mobilen Kamera entsprechend angewendet.

5.2.6   Berücksichtigung der Linsenverzeichnung

Das einfache, in Abbildung 5.1 beschriebene, Lochkameramodell bildet lineare homogene Weltkoordinaten in homogenen Bildkoordinaten ab. Die eingesetzten Kameras verfügen aber über ein Objektiv, dessen Linsensystem im Gegensatz zu einer Lochblende zu nicht linearen, radialen Verzerrungen führt (siehe Abbildung 5.2).

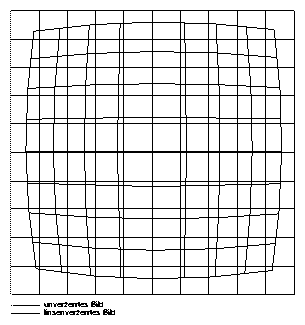
Wenn die Transformation nicht mehr genau genug durch eine lineare Transformation beschrieben werden kann, müssen Polynome höherer Ordnung für die Beschreibung eingesetzt werden. Polynome zweiter Ordnung werden häufig verwendet, um die geometrische Verzerrungseffekte zu beschreiben, wie sie durch Linsenverzerrungen entstehen. Im folgenden beschriebenen Verfahren [18] wird versucht für eine Korrektur der geometrischen Verzerrungen die tatsächlichen Bildkoordinaten (u,v) auf die gemessenen Bildkoordinaten (j,k) abzubilden.

Die Korrekturtransformation hat folgende Form:

wobei die Koeffizienten a₀,...,a₅ und b₀,...,b₅ Konstanten sind, welche die notwendige geometrische Korrektur beschreiben. Diese Koeffizienten können durch zwei Vektoren folgendermaßen beschrieben werden:

Ziel des Korrekturverfahrens ist die Minimierung des Fehlers zwischen den gemessenen und idealen Bildpunkten. Die quadratische Abweichung in Pixeln zwischen den idealen (j,k) und gemessenen Punkten (j¢,k¢) ist

Der Betrag eines Vektors x der Dimension m

kann verwendet werden, um den Fehler E für m Punkte zu beschreiben,

wobei j und k jeweils Vektoren der m Punktekoordinaten sind

und P eine Matrix ist, welche die Terme der zweiten Ordnung der beobachteten Bildpunkte enthält und definiert ist als:

Die Vektoren a und b , die den Fehler E des Korrekturverfahrens minimieren, können mit dem Verfahren der kleinsten Quadrate (siehe [24]) gefunden werden.

Man beachte das der Ausdruck ( P^TP) ^-1P^T in den Formeln 5.23 und 5.24 die bereits in Abschnitt 6 eingeführte Pseudoinverse der Matrix P darstellt.

Dieses Verfahren erlaubt eine Lösung des überdeterminierten Systems. Nur 6 Punkte sind notwendig, um Werte für die Vektoren a und b zu finden. Allerdings reduziert eine größere Anzahl von Punkten und eine Minimierung des Fehlers E die Abhängigkeit von statistischen Abweichungen.

5.3  Software zur Kamerakalibrierung

Für die Realisierung einer Kamerakalibrierungs-Software bietet sich die Verwendung von frei verfügbaren Bildverarbeitungsbibliotheken an. Es existieren einige umfangreiche Bildverarbeitungsbibliotheken, wie beispielsweise KOHROS, die für akademische Zwecke frei nutzbar sind. Allerdings ist keines dieser freien Pakete für das Betriebsystem OS9 zur erhältlich. Einige freie Bildverarbeitungsoftwarepakete stehen im Quelltext zur Verfügen, was eine Portierung auf OS9 ermöglicht. Der in Abschnitt 2.2.6 beschriebene GNU-C-Crosscompiler ermöglicht eine relativ einfache Portierung von Softwarepaketen. Allerdings muß bei einer Portierung, insbesondere auf ein Zielbetriebssystem wie OS9, welches in mehreren Hinsichten ein ,,Exot'' unter den Betriebssystemen ist, abgeschätzt werden ob der Aufwand hierfür nicht den Aufwand für eine neue Implementierung übersteigt.

Besonders günstig für eine mögliche Portierung auf OS9 sind Softwarepakete, die keine besonderen Anforderungen an zusätzliche Bibliotheken, oder an eine zu verwendende grafische Benutzeroberfläche stellen. Eine Implementierung der im UNIX-Umfeld weit verbreiteten grafischen Benutzeroberfläche XWINDOW ist zwar für OS9 verfügbar, aber sie hat sich als nicht netzwerkfähig und wenig kompatibel erwiesen.

Softwarepakete, die eine einfache Textkonsole voraussetzen, bzw. sich auf die einfache Implementierung von C-Libraries beschränken, sind komplizierteren Paketen für eine Portierung vorzuziehen.

Ein Bildverarbeitungs-Softwarepaket, das alle diese Forderungen erfüllt ist VIP [36].

5.3.1   Das Bildverarbeitungs-Softwarepaket VIP

VIP (Visual Information Processing) ist eine Bildverarbeitungs-Softwarebibliothek, die von der Robotics and Vision Research Group des Departement of Computer Science an der University of Western Autsralia entwickelt wurde.

Das System besteht aus zwei Teilen:

1. Einer Bibiliothek von C-Funktionen für die Manipulation und Transformation von Bildern, die für eigene Programme verwendet werden kann.
2. Einer Gruppe von ausführbaren Programmen für verschiedene, häufig benötigte Aufgaben in der Bildverarbeitung.

Die VIP-Bildverarbeitungsbibliothek ist speziell dafür angelegt worden, Benutzern auf einfache Weise zu ermöglichen, unter Verwendung einer standardisierten Bibliothek, eigene Bildverarbeitungsprogramme zu erzeugen.

Die Bibliothek beinhaltet Funktionen der folgenden Kategorien:

• Bild-Ein- und Ausgabe, Memorymanagement
• Bildtyp- und Datenformat Konvertierungen
• Bildverbesserung und Transformationen
• Maskenoperationen
• Arithmetische Operationen
• Statistische Bildverarbeitungsfunktionen
• Transformationen im Frequenzbereich
• Kamerakalibrierung und 3-D-Datenrekonstruktion
• Vektor- und Matrixoperationen
• Eindimensionale Kantendetektion
• Komplexe Arithmetik

Die VIP Bild-Datenstruktur unterstützt eine Reihe von Bildtypen, angefangen von einfachen 8 Bit Grauwertbildern, bis zu 24 Bit Farbbildern. Das VIP-eigene Bildformat integriert in seiner Datenstruktur Parameter, die die Kamera Kalibrierung und Linsenverzerrungsparameter beinhalten. Außerdem gewährleistet das VIP-System die 3-D-Bildverarbeitung mit strukturiertem Licht- und Stereokamerasystemen.

Nutzbar ist das VIP-System für die Betriebssysteme UNIX auf DEC ALPHA, SUN SPARC und LINUX, ein Teil der Funktionalität steht auch unter DOS auf PC's zur Verfügung [36].

5.3.2  Das Programm calibrate

Das VIP-System enthält das für die Berechnung vom Kamerakalibrierungen vorgesehene Programm calibrate.

Dieses Programm errechnet eine 3×4 Kamerakalibrierungsmatrix und optional ein Korrektur-Polynom dritter Ordnung für die Linsenverzeichnung. Die Eingabedaten des Programms sind eine Reihe 3-D-Koordinaten von Kalibrierungspunkten mit korrespondierenden 2-D-Koordinaten dieser Punkte. Das Programm gibt eine binäre Datei aus, welche eine CAMERA-Datenstruktur (siehe Anhang Seite pageref) enthält. Die CAMERA-Struktur umfaßt die gesamten Kalibrierungsergebnisse. Für eine Kontrollmöglichkeit wird eine Version dieser Kalibrierungsdaten in eine Text-Datei gespeichert. Das Programm erfragt beim Start die Dateinamen der Textdateien, welche die 3-D- und 2-D-Information enthalten. Alternativ können diese Informationen auch einer Bild-Datei im VIP-Format entnommen werden. Nach Berechnung der Kameramatrix wird diese auf der Konsole angezeigt und der Benutzer kann auswählen, ob er eine weitere Berechnung der Linsenverzeichnung für sinnvoll hält.

Wenigstens die Korrespondenzen von 6 Punkten müssen in den 3-D- und 2-D-Testdateien eingetragen sein, um eine Kamerakalibrierung zu ermöglichen (Siehe auch Ausdruck 5.9). Für eine erfolgreiche Berechnung der Linsenverzeichnungskoeffizienten müssen diese Punkte weit verteilt im beobachteten Volumen liegen. Wird eine größere Anzahl von Punkten verwendet, erreicht man eine größere Unempfindlichkeit gegenüber statistischen Ausreißern.

5.3.3   Die Bildverarbeitungsbibliothek vip.l

Die im Abschnitt 5.3.1 erwähnten Bibliotheksfunktionen für Kamerakalibrierung und 3D-Datenrekonstruktion beinhalten die folgenden, für die hier beschriebene Anwendung, relevanten Funktionen:

void xyz2uv(double xyz[3], int uv[2], CAMERA camera); 

Diese Funktion konvertiert (x,y,z) -Weltkoordinaten in (u,v) -Bildkoordinaten. Die Struktur CAMERA wird im Anhang aus Seite A.1 beschrieben. Sie enthält im wesentlichen die geeichte Kameramatrix der entsprechenden Kamera.

int Stereo_Point(double uv1[2], double uv2[2], 

CAMERA cam1, CAMERA cam2, double P[3]);

Diese Funktion berechnet (x,y,z) -Weltkoordinaten (P[3]) aus (u,v) -Bildkoordinaten von zwei Kameras⁴⁹.

int Lens_Comp_3(int iuv[ ], double duv[ ], 

CAMERA camera, int npts); 

Die Funktion Lens_Comp_3 berechnet die Korrekturfaktoren der Linsenverzerrung.

int Calibrate(double uv[ ][2], double xyz[ ][3], 

int npts, CAMERA camera, char *filename, int lenscomp);

Die Funktion calibrate errechnet aus 3-D-Weltkoordinaten und 2-D-Bildkoordinaten eine Kameramatrix.

int Read_Calib_Pts(char *filename, double CalibPts[ ][3], int *Npts); 

Diese Funktion liest 3-D-Kalibrierungsdaten aus einer Textdatei aus. Sie erwartet folgende Textformatierungen:

Dateibeschreibungen, Kommentare usw.

point 1 x y z 

point 2 x y z 

. . . . . 

point n x y z

Alle Zeilen der Datei werden ignoriert, außer sie beginnen mit dem Token ,,point''. Die Numerierung der Punkte ist nur für die Unterstützung des Benutzers vorgesehen, diese Ziffern werden ignoriert.

int Read_Image_Pts(char *filename, double ImagePts[ ][2], int *Npts); 

Diese Funktion liest 2-D-Kalibrierungsdaten aus einer Textdatei aus. Sie erwartet folgende Textformatierungen:

Dateibeschreibungen, Kommentare usw.

imagepoint 1 u v

imagepoint 2 u v

. . . . . . . . 

imagepoint n u v

Alle Zeilen der Datei werden ignoriert, außer sie beginnen mit dem Token ,,imagepoint''. Die Numerierung der Punkte ist nur für die Unterstützung des Benutzers vorgesehen, diese Ziffern werden ignoriert.

int Write_Camera_Txt(char *filename, CAMERA camera); 

Diese Funktion schreibt eine CAMERA-Datenstruktur in eine Textdatei.

CAMERA *Read Camera(char *filename); 

Diese Funktion liest ein binäres Kameradatenfile ein, speichert die Daten in einer CAMERA-Struktur und gibt einen Pointer auf diese Struktur zurück.

All diese Funktionen können verwendet werden, wenn die Header-Datei vip.h per #include-Anweisung in eigene Programme eingebunden wird.

Das endgültig ausführbare Programm muß dann mit der Bibliothek vip.l gelinkt werden.

5.3.4  Portierung auf OS9

Für die Portierung auf OS9 mußten folgende Dateien angepaßt werden:

Modifikationen für das vip.l Library:
Im Verzeichnis include/

• vip.h
• values.h 

Im Verzeichnis src/lib/

2

• Makefile
• vipcalib.c
• misc.c
• oldvip.c
• pm.c
• ppmrgb.c
• rast.c
• vector.c
• vipcomplex.c
• vipio.c
• vipspat.c 

 
Im Verzeichnis src/vip/

• Makefile

Folgende Funktionen stellt das C-Library von OS9 nicht zur Verfügung:

• strcasecmp()
• strdup()

Diese Funktionen mußten für OS9 nachgebildet werden. Ein Großteil der Modifikationen betrifft Header-Dateien, die OS9 nicht oder anders zur Verfügung stellt. Andere Anpassungen betrafen prozessorspezifische Details ( Little Endian, Big-Endian). Die Makefiles mußten für die Verwendung des Crosscompilers für OS9 stark verändert werden.

Insgesamt konnte die Portierung von VIP nach OS9 mit vertretbarem Aufwand realisiert werden.

5.4  Praktischer Ablauf der Kamerakalibrierung

Das beschriebene Library und das calibrate-Programm wurden in die erstellte Software integriert, so daß sich zwei verschiedene Verfahren der Kamerakalibrierung realisieren ließen.

Die Kamerakalibrierung muß für beide Kameras vorgenommen werden. Ändert sich die Orientierung oder die Brennweite einer Kamera, so muß die Eichung für diese Kamera wiederholt werden.

5.4.1   Einsatz eines Eichkörpers

Die klassische Methode der Eichung ist die Verwendung eines Eichkörpers, der vermessene Eichmarken enthält, deren 3-D-Koordinaten bekannt sind. Der Ursprung des verwendeten Welt-Koordinatensystems kann prinzipiell frei gewählt werden, zweckmäßigerweise wird aber der Ursprung in den Maschinennullpunkt des Industrieroboters gelegt. Der verwendete Eichkörper besteht aus einer geschwärzten quadratischen Grundplatte, in die 16 Stangen unterschiedlicher Länge eingelassen sind, deren oberer Querschnitte mit weißen Eichmarken versehen sind. (siehe Abbildung 5.3)

*0.9!

Die Geometrie des Eichkörpers ist in einer Textdatei in dem für die VIP-Bibliothek lesbaren Format abgelegt. Diese mit einem Texteditor erzeugte Datei hat folgenden einfachen Aufbau:

# 3-D-Eichfile fuer den Eichkoerper 1 

# 

# Ursprung ist der auf der Rueckseite des Eichkoerpers mit 

# 0 bezeichnete Punkt, X UND Y-Achsen sind dort ebenfalls angegeben 

# 

# 0 --->x 

# | 1 2 3 4 

# v 5 6 7 8 

# y 9 10 11 12 

#  13 14 15 16 

# 

# 

# Entfernung des Punktes 0 von dem naechsten Eckpunkt der Grundplatte: 

# Xo= 50 mm Yo= 50 mm 

# Dicke der Grundplatte: 12.7 mm , Z-Koordinatenursprung ist die 

# obere Flaeche der Grundplatte 

# Punkt 1 liegt auf der Kooedinate x=0 und y=0 

# 

point 1 0 0 130 

point 2 100 0 140 

point 3 200 0 150 

point 4 300 0 160 

point 5 0 100 20 

point 6 100 100 60 

point 7 200 100 100 

point 8 300 100 140 

point 9 0 200 100

point 10 100 200 60 

point 11 200 200 60 

point 12 300 200 120 

point 13 0 300 20 

point 14 100 300 100 

point 15 200 300 20 

point 16 300 300 100

Das Format dieser Datei entspricht dem im Abschnitt 5.3.3 erläuterten Eingabeformat der VIP-Bibliotheksfunktion Read_Calib_Pts.

Nach dem Start aller Bildverarbeitungskomponenten wird der Eichkörper im Arbeitsraum positioniert. Dann werden die jeweils 16 Koordinaten der erkannten 2-D-Objekte aus den beiden IC40-Bildverarbeitungskarten ausgelesen, für alle 2-D-Objekte die Mittelpunktkoordinaten bestimmt und abschließend in zwei Textdateien geschrieben.

Die 2-D-Kameraeichdateien, deren genaues Format im Abschnitt 5.3.3 erläutert wird, müssen die Eichpunkte in der gleichen Reihenfolge enthalten, wie sie in der obigen 3-D-Eichdatei angegeben sind, um die notwendigen Korrespondenzen herzustellen. Da zu diesem Zeitpunkt noch keine Kameraeichung⁵⁰ vorhanden ist, kann diese Zuordnung manuell oder mit einem heuristischen Algorithmus, welcher eine festgelegte Orientierung der Kameras relativ zum Eichkörper erfordert, ermittelt werden. Eine auf diese Weise automatisierte Eichung ist einer manuellen Vorgehensweise vorzuziehen, weil ein neuer Eichvorgang bei jeder Änderung der Orientierung der Kameras notwendig ist. Für den eingesetzen Eichkörper ist ein solcher heuristischer Algorithmus implementiert worden, allerdings muß dieser für stark veränderte Kamerapositionen bzw. Eichkörper neu angepaßt werden.

Nachteil des verwendeten Eichkörper ist es, daß nicht der gesamte Arbeitsraum des Industrieroboters abgedeckt wird, ein so großer Eichkörper wäre allerdings schwer zu handhaben.

Sind beide 2-D-Dateien und die notwendige 3D-Textdatei erzeugt worden, wird durch Systemaufrufe zweimal⁵¹ das Programm calibrate aufgerufen, welches die Berechnung der Kameramatrix und optional der Linsenverzeichnung ausführt. Schließlich werden beide binären Ausgabedateien der calibrate-Durchläufe in das realisierte Programm eingelesen und für die kontinuierliche Berechnung von 3-D-Weltkoordinaten verwendet.

5.4.2  Einsatz des Industrieroboters zur Kamerakalibrierung

Bildverarbeitungssysteme werden unter anderem auch für die Kalibrierung von Industrierobotern eingesetzt [14]. Daher liegt der Gedanke nahe, umgekehrt den zu überwachenden Industrieroboter für eine Kamerakalibrierung einzusetzen. Die Robotersteuerung teilt der überwachenden Haupt-CPU kontinuierlich die aktuellen Ist-Positionen des Tool-Center-Points des Industrieroboters mit. Somit lassen sich diese Informationen nutzen, um mit einer in der Nähe des TCP⁵² angebrachten Eichmarke verschiedene Raumpunkte im Arbeitsraum des Roboters anzufahren, deren Koordinaten dann für die Kamerakalibrierung genutzt werden.

*0.9!

Zu diesem Zweck ist ein Verfahren implementiert worden, daß es erlaubt, mittels einer an eine serielle Schnittstelle der Haupt-CPU-Karte angeschlossenen 3-D-Steuerkugel, Eichpositionen zu teachen, die in einem VIP-konformen Textfortmat abgespeichert werden können.

Der implementierte Eichvorgang kann so vollkommen automatisch abgearbeitet werden. Die 3-D-Eichdatei wird eingelesen und der in Abschnitt 3.1beschriebene Bahninterpolator führt den Industrieroboter an die angegebenen 3-D-Positionen. Die aktuellen 2-D-Koordinaten der Eichmarke werden jeweils aus beiden IC40-Karten ausgelesen.

Wenn alle Positionen angefahren worden sind liegen die vollständigen 2-D-Koordinaten in der richtigen Reihenfolge vor und können so in die beiden VIP-konformen 2-D-Eichdateien geschrieben werden. Die Korrespondenzauflösung erfolgt hier automatisch durch die festgelegte zeitliche Abfolge in der die Eichmarke an verschiedenen Positionen beobachtet wird. Die weitere Vorgehensweise unterscheidet sich nicht von der im Abschnitt 5.4.1.

Dieses Verfahren hat folgende Vorteile gegenüber der Verwendung eines Eichkörpers:

• Korrespondenz durch zeitliche Abfolge
• Die Koordinaten liegen sofort im Roboterkoordinatensystem vor und betreffen den für die Kollisionsvermeidung kritischen Extrempunkt
• Der gesamte Roboterarbeitsraum kann vermessen werden
• Eventuelle Positionsfehler des Roboters heben sich auf
• Robust und einfach. Im Gegensatz zur Verwendung eines Eichkörpers verschwindet bei Beleuchtungsschwankungen nur ein Eichpunkt, dessen Wiedererscheinen in den 2-D-Bildern, das Eichprogramm einfach abwartet. Es ergeben sich durch verschwindende Eichpunkte keine fatalen Auswirkungen auf eine Korrespondenzbildung

Mit dieser Kamerakalibrierung ist ein für die betrachtete Problemstellung günstiges und robustes Verfahren implementiert worden.

5.5  Das Korrespondenzproblem

Die Korrespondenzauflösung zwischen zwei 2-D-Bildern ist kein triviales Problem. Allgemein lassen sich die in der Literatur beschriebenen Verfahren [19] [25][27] im wesentlichen einteilen in

• Merkmalsbasierte Stereoverfahren
  Diese Verfahren versuchen die Korrespondenzauflösung anhand symbolischer Merkmale die aus Grauwertbildern gewonnen werden.
• Lokale Flächenbasierte Verfahren
  Diese Verfahren vergleichen limitierte Korrespondenzfenster in beiden Grauwertbildern, um Regionen mit sehr ähnliche Grauwertverteilung zu finden. Nachteil dieses Verfahrens ist die Lokalisierungsunschärfe. Die Größe der jeweiligen Kontrollfenster für die Berechnung der Grauwertverteilung, begrenzt die maximal ermittelbare Disparität (siehe Abbildung 5.5).
• Aktive Verfahren
  Aktive Verfahren wie Kamera-Projektor-Anordnungen mit bekannter Projektions- und Abbildungsstrahlengeometrie, oder Lichtschnittverfahren. Diese Verfahren ermöglichen durch die Projektion einzelner Punkte oder Linien eine einfach Korrespondenzauflösung.
  *0.9!
  
  Figure 5.5: Disparität

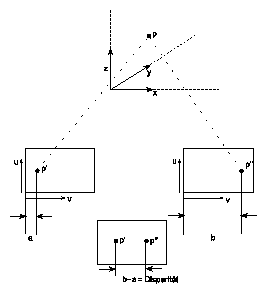
Die Korrespondenzauflösung mit Hilfe von merkmalsbasierten Verfahren wird häufig durch die Epipolarlinienbedingung auf ein eindimensionales Problem reduziert. Die Epipolarlinienbedingung fordert, daß korrespondierende Punkte in beiden Bildern eines Stereokamerasystems auf den Epipolarlinien liegen müssen, die durch den Schnittpunkt der Epipolarebene mit der Abbildungsebenen der Sensoren gebildet werden. Die Epipolarebene wird durch den Raumpunkt und die beiden Abbildungspunkte auf den Kamerasensoren aufgespannt (siehe Abbildung 5.6).

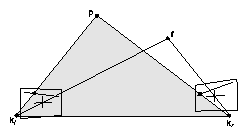
Das hier beschriebene Verfahren der Kamerakalibrierung ermittelt allerdings nicht die externen Kameraparameter wie Position und Orientierung, so daß ein anderer Ansatz verfolgt werden muß.

Wenn identische Kameras (gleiche Brennweite, interne Kameraparameter, usw.) auf gleicher Höhe parallel den Arbeitsraum überwachen, liegen die korrespondierenden Punkte in der gleichen Bildzeile und das Suchproblem wird eindimensional.

Zwei dieser Bedingungen sind in etwa erfüllt, die Kameras sind allerdings gegeneinander geneigt, damit der Phantombereich des Stereokamerasystems minimiert wird. Korrespondierende Punkte sollten in der gewählten Anordnung tatsächlich in ähnlichen u -Bildzeilenkoordinaten liegen. Außerdem sollte bei einem recht großen vertikalen Abstand vom Arbeitsraum, bzw. einer kleinen Brennweite der Kameras, die relative Größe der 2-D-Objekte in u unter den genannten Bedingungen auf beiden Sensorebenen sehr ähnlich sein.

Mit diesen beiden Bedingungen wird eine Suche nach ähnlichen 2-D-Objekten durchgeführt. Es handelt sich bei den von den IC40-CPU-Karten vereinfachten 2-D-Objekten um solche, mit nur zwei Extremwerten. Diese können anhand ihrer Größen und ihrer Position leicht einander zugeordnet werden. Sind die Korrespondenzen zweier Objekte anhand ihrer zu ähnlichen u -Lage und u -Ausdehnung nicht aufzulösen wird aus diesen beiden Objekten ein einziges größeres generiert, deren Korrespondenzen sich nun einfacher auflösen lassen. Diese einfache heuristische Korrespondenzauflösung ist für das beschriebene Problem ausreichend, da hier keine genaue Vermessung des Arbeitsraums erforderlich ist, sondern für die Zwecke der Kollisionsvermeidung die ungefähre Lage eines Hindernisses erkannt werden soll. Wenn die dreidimensionale Ausdehnung eines Hindernisses durch ein solches Stereoverfahren überschätzt wird, ist dieses für eine Anwendung der generierten 3-D-Daten für eine Kollisionsvermeidung unkritisch.

5.5.1  Auswirkungen der Verktorisierung auf die Korrespondenzauflösung

Durch den Einsatz der Vektorisierungskarten in der 2-D-Bildverarbeitung ergeben sich folgende Probleme für die Erkennung markanter Punkte, die sich für eine Korrespondenzauflösung eignen.

Das in Abschnitt 4.8 erläuterte Vektorisierungsverfahren bricht die Vektorisierung einer Teilkontur immer ab, wenn der aktuelle Vektor um einen bestimmten Winkel von der Kontur abweicht, um dann einen neuen Vektor zu erzeugen. Diese, sich durch die Vektorisierung ergebenden, markanten Punkte (Stellen an denen ein neuer Vektor begonnen wird) korrespondieren bei Objekten, die nicht über scharfe Knickstellen in ihrer Kontur verfügen, nicht miteinander in verschiedenen 2-D-Ansichten.

Das eingesetzte vereinfachende 2-D-Objekterkennungsverfahren (siehe Abschnitt 4.9) berechnet nur die Extremwerte der 2-D-Objekte. Eine Korrespondenzauflösung dieser eventuell nur virtuell existierender Extremwerte (siehe Abbildung 5.7)

*0.9!

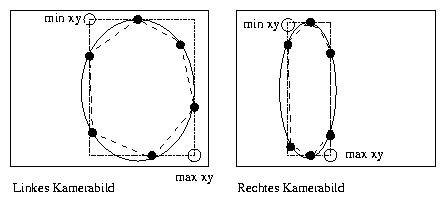
ist sehr einfach, allerdings führt die 3-D-Bearbeitung solch virtueller, außerhalb der Objektkontur liegender Punke, zur Detektion einer zu großen dreidimensionale Ausdehnung eines Objektes. Wenn die dreidimensionale Ausdehnung eines Hindernisses durch ein solches Stereoverfahren überschätzt wird, ist dieses für eine Verwendung der generierten 3-D-Daten für eine Kollisionsvermeidung unkritisch.

Das in Kapitel 7 beschrieben Kollisionsvermeidungsverfahren basiert auf unscharfer Fuzzy-Logik, weshalb an dieser Stelle kein zu hoher Genauigkeits-Aufwand getrieben werden soll.

Untersuchungen über die mit diesem einfachen Ansatz einer Stereobildverarbeitung zu erreichende Genauigkeiten werden im Abschnitt 9 angestellt.

Kapitel 6
Kollisionsvermeidung

Unter dem Begriff Kollisionsvermeidung versteht man die Überwachung von Werkzeugmaschinen und Industrierobotern auf Kollisionen mit Werkstücken, Hindernissen oder weiteren Werkzeugmaschinen, bzw. Industrierobotern, und die Vermeidung dieser Risiken.

Es können zwei grundsätzlich verschiedene Verfahren zur Kollisionsvermeidung unterschieden werden.

1. Offline-Kollisionsvermeidung:
   Bei einer Offline-Kollisionsvermeidung werden die Ergebnisse einer Offline-Bahnplanung auf Kollisionen hin untersucht, um solche Risiken auszuschließen. Werkzeugmaschinen werden heutzutage vorwiegend noch offline programmiert, d.h. die Programmerstellung erfolgt in Programmierabteilungen. Wenn alle involvierten Prozesse im fertigungsablauf determiniert werden können, ist eine Offline-Bahnplanung auch für Industrieroboter sinnvoll. Werden allerdings im Zuge vom Einsatz flexibler Fertigungsverfahren häufige Änderungen in Produktionsabläufen nötig, bzw. ist die Produtionsabfolge nicht mehr determistisch festgelegt, kann die Offline-Bahnplanung keine Kollisionsvermeidung mehr einschließen.
2. Online-Kollisionsvermeidung:
   Sollen die Komponeten einer Arbeitszelle allerdings flexibel auf sich verändernde Taktzeiten reagieren, wie sie zum Beispiel durch statistische Schwankungen im Fertigungsprozeß auftreten, ist eine Online-Bahnplanung in Verbindung mit einer Online-Kollisionsvermeidung notwendig. Eine Sensorik, wie die hier beschriebenene Stereo-Bildverarbeitung kann verwendet werden, um Kollisionsgefahren mit Hindernissen oder Kollisionen durch Soll- und Istwertdifferenzen von mehreren, in einer Fertigungszelle arbeitenden, Industrierobotern zu erkennen und zu verhindern. Eine Online-Kollisionsvermeidung muß aus diesem Grund Echtzeitanforderungen erfüllen.

Online-Kollisionsvermeidungsverfahren gewinnen im Zuge der fortschreitenden Automatisation und durch den Einsatz flexibler Fertigungsverfahren zunehmend an Bedeutung.

6.1  Kollisionsvermeidungsverfahren für 6-Achsen Industrieroboter

Industrieroboter mit 6-Achsen stellen besondere Anforderungen an Kollisionsvermeidungsalgorithmen, da aufgrund ihrer Kinematik ( kinematische Ketten) nicht nur der Greiferort, sondern auch die Lagen des Ellbogens im Unter- und Oberarm und der Schulter des Robotors in die Ermittlung von kollisionsfreien Trajektorien eingehen müssen. Es existieren Verfahren, die die Kinematik eines 6-Achsen Indutrieroboters auf ein einfacheres Modell, dem sogenannten ,,Reduzierten Aktuellen Roboter'' (R.A.R), abbilden, um die Ermittlung von kollisionsfreien Trajektorien zu vereinfachen.[26] Dieses Verfahren ist eine konsequente Weiterentwicklung des ürsprünglich in [29] vorgestellten Verfahrens, das in [30] auf Mehrrobotersysteme erweitert worden ist.

In [26] ist ein Fuzzy-Logik basierter Ansatz für die Kollisionsvermeidung von 6-Achsen Industrierobotern vorgestellt worden. Das dort beschriebene Verfahren der Kollisionsvermeidung zweier Roboter mit sich überschneidenden Arbeitsräumen wird in dieser Arbeit für einen einzelnen Roboter vereinfacht eingesetzt.

Weitere Vereinfachungen des hier eingeführten Verfahrens betreffen die Beschränkung der Überwachung auf den Tool-Center-Point (TCP) des Industrieroboters. Für eine Erläuterung der behandelten Problematik ist eine kurze Einführung in die für die Beschreibung von Robotern verwendeten Koordinatensysteme und Transformationen notwendig.

6.2  Roboterkoordinatensysteme

Für die mathematische Modelierung einer Roboterkinematik werden den Gliedern des Roboterarmes körperfeste Koordinatensysteme zugeordnet.

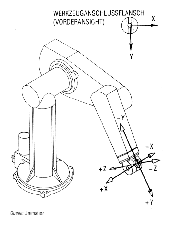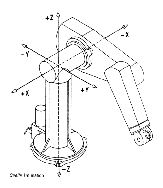Die bereits in Abschnitt 5.2.1 eingeführten homogenen Koordinaten können dazu verwendet werden, die Lage eines Koordinatensystems relativ zu einem Referenzsystem darzustellen. Die Denavit-Hartenberg Notation beschreibt den Übergang von einem Gliedkoordinatensystem T_i-1 zu einem nachfolgende Gliedkoordinatensystem T_i eines Roboters. Die homogene 4×4 Transformationsmatrix A_i , welche diesen Übergang beschreibt, wird durch die vier Denavit-Hartenberg Parameter j_i,d_i,a_i und a_i
folgendermaßen definiert[31]:

Die Matrix A_i stellt die reduzierte Form der homogenen Tranformation durch zwei Translationen a_i und d_i und zwei Rotationen j_i und a_i dar. Die Greiferstellung T_g erhält man nun in Basiskoordinaten durch Multiplikation aller 4×4 Matrizen A_i . (Für einen 6-Achsen Roboter ergeben sich also 6 Transformationsmatrizen)

Die verwendete Robotersteuerung teilt dem Bildverarbeitungrechner kontinuierlich die Position des Tool-Center-Point bzw. die Greiferstellung in folgender Notation als Transformationsmatrix mit:

Wobei p_x,p_y,p_z die Position des Greifers und die Einheitsvektoren i_g,j_g,k_g die Orientierung des Greifers bezüglich eines raumfesten Koordinatensystems beschreiben. Da die gewählte Realisation der Kollisionsvermeidung nur die Position des TCP auswertet, ist eine Rücktransformation auf entsprechende Roboterglieder hier nicht erforderlich. Das vorgestellte Konzept kann aber in dieser Hinsicht erweitert werden. Die erwähnte Rücktransformation würde die Auflösung von Mehrdeutigkeiten und Singularitäten der Gelenkpositionen bedingen.

In Abschitt 7.3 wird die hier eingesetzte Fuzzy-Kollisionsvermeidungsstrategie ausführlich beschrieben. Es folgt zunächst eine kurze Einführung in die Thematik ,,Fuzzy Control''.

Kapitel 7
Fuzzy Control

,,Fuzzy'', auf deutsch ,,fusselig, verschwommen'', wird in diesem Kontext günstigerweise als ,,unscharf'' übersetzt. Die in den 60'er Jahren von Zadeh entwickelte Theorie unscharfer Mengen soll hier nicht näher erläutert, sondern nur auf für die Implementierung notwendige Details eingegangen werden. Eine Umfangreiche Einführung findet sich in [35].

7.1  Fuzzy-Control für die Kollisionsvermeidung

Das realisierte Kollisionsvermeidungskonzept umfaßt die in Abbildung 7.1 aufgeführten Komponenten.

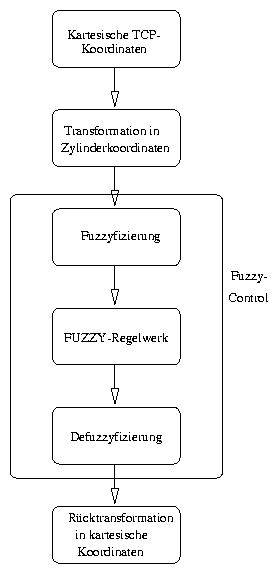
Stichwortartig verkürzt sollen hier die Schritte einer Fuzzy-Regelung erläutert werden (siehe [35]):

1. Fuzzyfizierung
   Unter Fuzzyfizierung versteht man die gewichtete Zuordnung eines ,,scharfen'' Meßwertes zu ,,unscharfen'' linguistischen Termen aus vordefinierten Fuzzy-Mengen. Man erhält einen Vektor m(x) von Zugehörigkeitsgraden m_i(x) zu den definierten linguistischen Termen.
   1. Eine linguistische Variable ist eine Kenngröße des betrachteten Prozesses
   2. Ein linguistischer Term ist die umgangssprachliche Beschreibung eines Zustandes des betrachteten Prozesses (z.B. klein, groß, usw.)
   3. Fuzzy-Mengen sind unscharfe Mengen die einen linguistischen Term beschreiben
   4. Zugehörigkeitsgrade: Ein ,,scharfer'' Wert gehört verschiedenen, sich überschneidenden, Fuzzy-Mengen zu verschiedenen Graden an

2. Fuzzy-Regelbasis, Inferenz
   Werden auf Zugehörigkeistsfunktionen umgangssprachliche WENN-DANN-Regeln angewandt, enstehen neue Ergebnismengen, abhängig davon, ob eine Verknüpfung mit UND (Schnittmenge) oder ODER (Vereinigungsmenge) stattfindet.
3. Defuzzyfizierung
   Mit Defuzzyfizierung wird derjenige Vorgang bezeichnet, der Ergebnismengen der Inferenz wieder auf ,,scharfe'' Ausgabewerte abbildet. Weil die Ergebnismengen der Inferenz geometrisch als Schnitt,- oder Vereinigungsmenge betrachtet werden, können auf verschiedene Weisen aus diesen Ergebnisflächen ,,scharfe'' Ausgangswerte gewonnen werden. Zu nennen sind die Flächenschwerpunkt- und die Maximum-Mittelwert-Methode.

7.2   Die eingesetzten Werkzeuge

Für die Modellierung der hier beschriebenen Fuzzy-Kollisionvermeidung wurde das FOOL-Paket [32] eingesetzt. FOOL, der ,,Fuzzy Organizer OLdenburg'' ist ein Softwarepaket, das an der Universität Oldenburg entwickelt wurde. FOOL erlaubt die Modellierung von Fuzzy-Regelungen mit einer einfach zu bedienenden grafischen Benutzeroberfläche.

Linguistische Variablen können ebenso wie eine Regelbasis einfach erzeugt und editiert werden. Die verwendeten lingustischen Terme können grafisch angezeigt werden. Den modellierten Fuzzy-Regler speichert FOOL in einem speziellen Textformat ab, so daß Projekte weiterbearbeitet, bzw. modifiziert werden können.

Ursprünglich wurde FOOL in C entwickelt, die aktuelle C-Version 1.33 enthält allerdings noch einige Fehler, die z.B. ein Arbeiten mit linguistischen Variablen verhindern, deren Grenzen keine ganzen Zahlen sind. Die JAVA-Version von FOOL (Vers. 2.1 alpha 3) läuft allerdings stabil.

Der mit FOOL entwickelte Fuzzy-Regler kann mittels des Zusatzprogrammes FOX ,,Fuzzy Organizer Executor'' getestet und eingesetzt werden. FOX liest den modellierten Fuzzy-Regler aus der mit FOOL generierten Textdatei ein und fuzzyfiziert Eingabewerte, welche über Komandozeilenparameter übergeben werden können. Die Inferenzmaschine von FOX arbeitet das Fuzzy-Regelwerk ab und, abhängig von einem mittels Komandozeilenparameter übergebenen Flag, werden Fuzzy oder defuzzyfizierte Ausgangswerte ausgegeben.

Eine relativ neue Zusatzentwicklung ist FolToC [33], ein Programm, welches aus dem mit FOOL modellierten Fuzzy-Regler-Dateien C-Programmcode generieren kann. Dieser C-Programmcode läßt sich problemlos in das hier beschriebene Kontrollprogramm integrieren.

Über die grafische Benutzeroberfläche von FOOL können Änderungen am Fuzzy-Regler für die Kollisionsvermeidung vorgenommen und im Quellverzeichnis der Kontrollsoftware abgespeichert werden. Ein make-Aufruf aktualiesiert dann automatisch den im Kontrollprogramm enthaltenen Fuzzy-Regler⁵³.

7.3   Die Fuzzy-Kollisionsvermeidungsstrategie

Die hier beschriebene Fuzzy-Kollisionsvermeidung setzt ein wenn die Bildverarbeitungssensorik ein Hindernis innerhalb einer bestimmten Entfernungsschwelle um den TCP detektiert.

Für das gegebene Kollisionsvermeidungsproblem ist es günstig in Anlehnung an [26] zunächst nur den Tool Center Point des sechsachsigen Industrieroboters in einem zylindrischen 3D-Koordinatensystem zu betrachten. Der Winkel und der Radius im zylindrischen Koordinatensystem sind dann die entsprechenden linguistischen Variablen für dieses Problem. Die in diesem Koordinatensystem gewählten linguistischen Terme sind in Abbildung 7.2 visualisiert.

Die Koordinatenen des TCP wurden also vor der Fuzzyfizierung in Zylinderkoordinaten transformiert. Nach der Defuzzyfizierung ist dann eine Rücktransformation der Zylinderkoordinaten in Kartesische notwendig.

*0.9!

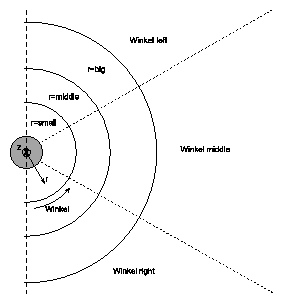
Für die linguistischen Variablen können zweckmäßigerweise folgende Parameter gewählt werden:

• Radialkomponente des TCP bezogen auf den Ursprung eines zylindrischen Koordinatensystems
• Winkelkomponente des TCP im zylindrischen Koordinatensystem
• Höhenkomponente des TCP im zylindrischen Koordinatensystem
• Radialkomponente eines beobachteten Hindernisses im zylindrischen Koordinatensystem
• Winkelkomponente eines beobachteten Hindernisses im zylindrischen Koordinatensystem
• Höhenkomponente eines beobachteten Hindernisses im zylindrischen Koordinatensystem

In einem ersten Ansatz wird auf die Integration der Höhenkomponenten in den Fuzzyregler verzichtet. Allerdings wird bei Detektion eines potentiellen Kollisionsrisikos durch die 3-D-Bildverarbeitung der TCP in der Höhenkomponente so verfahren, daß eine Position erreicht wird, die wenig anfällig für Singularitäten der Roboterachsen ist.

Es wurden zunächst verschiedenen Fuzzyregler für die Winkel- und Radialkomponenten realisiert. Es hat sich gezeigt, daß bereits ein relativ günstiges Verhalten erreicht werden kann wenn nur die Radialkomponente der Roboterbewegung durch einen Fuzzy-Regler beeinflußt wird.

7.4  Die Fuzzy-Sets für die Berechnung der Radialkomponente

Mit dem gewählten Ansatz verbleiben vier linguistische Variablen für die Modellierung der Fuzzy-Sets:

• Objekt-Radialkomponente mit den linguistischen Termen small, middle und big, siehe Abbildung 7.3
• Kollisionsobjekt-Winkelkomponente mit den linguistischen Termen left, middle und right, siehe Abbildung 7.4
• Roboter-Radialkomponente mit den linguistischen Termen small, middle und big, siehe Abbildung 7.5
• Roboter-Winkelkomponente mit den linguistischen Termen left, middle und right, siehe Abbildung 7.6

7.5  Die Fuzzy-Regelbasis

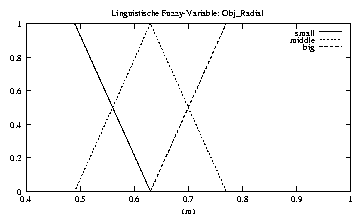
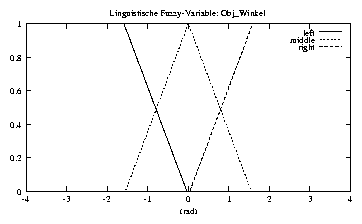
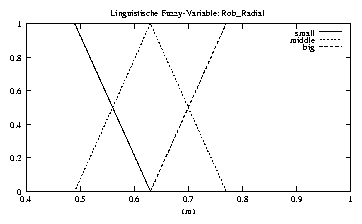
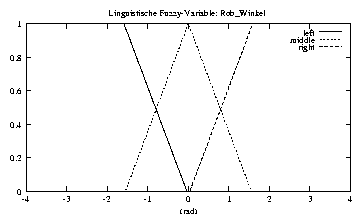
Die für die Kollisionsvermeidungsstrategie gewählten Inferenzen gibt die Abbildung 7.7 in der in FOOL üblichen Darstellung wieder.

*1.2!

7.6  Die Defuzzyfizierung

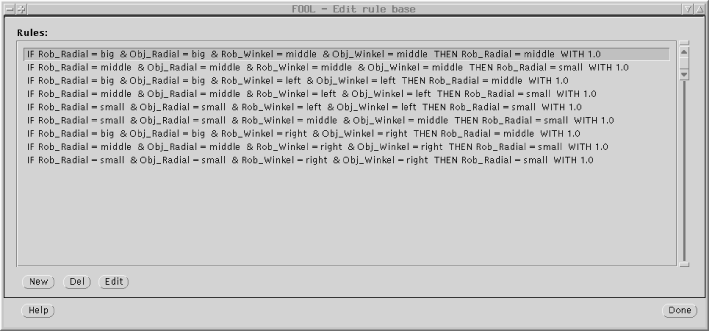
Die Defuzzyfizierung wird im beschriebenen Ansatz aus Geschwindigkeitsgründen mit der ,,Mean of Maximum''-Methode vorgenommen. Mit dieser Methode ergibt sich ein erheblicher Geschwindigkeitsvorteil der Berechnung gegenüber dem Verfahren ,,Center of Gravity''. Die Defuzzyfizierungsmethode kann der Benutzer in FOOL unter mehreren Alternativen auswählen. Der beschriebene Geschwindigkeitsunterschied ist deshalb so hoch, weil FOOL bzw. FolToC Fuzzy-Sets intern als diskrete Wertepaare ( Singletons) und nicht als parametrische Darstellung in Form analytischer Funktionen abspeichert, bzw. bearbeitet.

7.7  Die erreichte Funktionalität

Der einfache realisierte Fuzzycontroller ist in der Lage, Hindernissen auszuweichen und versucht weiterhin sein Ziel zu erreichen. Die generierten Trajektorien sind sicherlich nicht die für den jeweiligen Fall günstigsten, aber es wird im Allgemeinen eine Lösung des Kollisionsvermeidungsproblem gefunden. Kann der Fuzzy-Contoller keine Trajektorie mehr angeben, verharrt der Roboter aufgrund übergeordneter Kontrollstrukturen an seiner Position, bis wieder neue Handlungsmöglichkeiten entstehen. Insbesondere die in Abschnitt 7.3 erläuterte Strategie, bei drohenden Kollisionen immer auf eine für Singularitäten unempfindlichere Höhe zu verfahren, hat sich bewährt.

Das hier beschriebene Verfahren kann durch die zukünftige Berücksichtigung von Geschwindigkeiten des Roboters bzw. der Hindernisse noch wesentlich verbessert werden.

Kapitel 8
Die realisierten Softwarekomponenten

Im Rahmen dieser Arbeit sind folgende Softwarekomponenten erstellt worden:

1. Ein Kommunikationsmodul und ein Bahninterpolator für das in [11] beschriebene Robotersteuerungs-Kommunikationsprogramm
2. 2-D-Bildverarbeitungsprogramme für die IC-40 Bildverarbeitungskarten
   Dieses Progamm kommuniziert mit den Vektorisierungskarten und dem Kontrollprogramm
3. Ein Test- und Initialisierungsprogramm für 3-D-Bildverarbeitung
   Dieses Programm kommuniziert mit den 2-D-Bildverarbeitungsprogrammen
4. Ein Kontrollprogramm das die Kommunikation mit den 2-D-Bildverarbeitungsprogrammen (2.) und die Kommunikation mit dem Robotersteuerungsprogramm (1.) mit weiteren Funktionen integriert

Das erstellte Kontrollprogramm für eine Echtzeit-Kollisionsvermeidung, realisiert folgende Einzelfunktionalitäten:

• Kommunikation über ein OS9-Datenmodul mit dem Echtzeit-Robotersteuerungs-Kommunikationsprozeß
• Kommunikation mit beiden IC40-Bildverarbeitungskarten
• Automatisierter Eichvorgang für die Kamerasysteme
• Initialisierung der Bildverarbeitungskarten
• Generierung von 3-D-Daten aus den vorliegenden 2-D-Koordinaten
• Überprüfung auf Hindernisse und Kollisionsgefahren für den Industrieroboter
• Fuzzy-Kollisionsvermeidung mit dem integrierten, durch FolToC erzeugten, Fuzzy-Regler
• Abarbeitung von Bewegungssätzen
• Teachen von Bewegungssätzen
• Kontrolle der Eichung

*0.9!

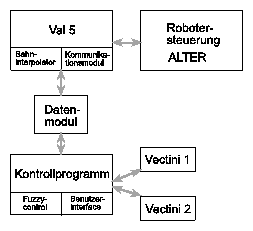
Die Abbildung 8.1 ermöglicht einen Umfassenden Überblick über die realisierten Softwarekomponenten und ihre Kommunikation untereinander.

8.1  Benutzeroberfläche des Kontrollprogramms

Das Kontrollprogramm besitzt die folgende textorientierte Oberfläche:

|--------------------------------------|-EXT-Systemmessg----------------------|

|                                      |Val5 PID: 17                          |

|                                      |                                      |

|                                      |                                      |

|                                      |                                      |

|                                      |                                      |

|-VAL-Altb-|-VAL-Ctrlb----|-DEBUG------|--------------Transformation----------|

|          |              |                      |                            |

|          |              | v[0]=0 d[0]=1        |-0.43 -0.90 -0.01 -177.65   |

|          |              | v[1]=0 d[1]=0        |-0.90  0.43  0.05  654.0    |

|          |              | v[2]=0 d[2]=0        |-0.04  0.02 -0.99 -456.00   |

|          |              | Fall:1               |                            |

|          |              | Fall:1               |                            |

|          |              | Fall:1               |                            |

|          |              | v[5]=0 d[5]=433      |                            |

|          |              |                      |                            |

|-3D Bildverarbeitung---------------------------------------------------------|

|Anz.O.G1:1 Frame:119804 Anz.O.G2:1 Frame:119802 Korresp:1 Obj1:1 Obj2:1 Kri:0|

|     min: -195.60325166 | 662.22414216  | -451.07710572                      |

|     max: -182.58415609 | 651.17940893  | -457.05421241                      |

|-CMD-------------------------------------------------------------------------|

|(S)tart Anz. (F)ahr (K)ont. (I)ni-Bild. (Z)ielpos. k(U)gel (O)pt. (Q)uit >   |

|-----------------------------------------------------------------------------|

Kapitel 9
Eine beispielhafte Kamerakalibrierung

In diesem Kapitel werden die Daten einer beispielhaften Kamerakalibrierung ausgewertet.

9.1  3-D-Eichkoordinaten

Die folgende Tabelle enthält die x,y und z Koordinaten einer Eichfahrt mit 45 Punkten:

# Eichfahrt fuer 3-D-Kamerakalibrierung, erzeugt mit Teach-Eichfahrt 

# Verlassen von umacs mit ctrl-X-C 

# point N X Y Z point 1 -181.593750 660.656250 -456.000000 

point 2 -178.562500 618.781250 -576.000000 

point 3 -299.531250 618.562500 -576.000000 

point 4 -302.656250 546.500000 -576.000000 

point 5 -431.437500 546.031250 -576.000000 

point 6 -428.937500 377.750000 -576.000000 

point 7 -104.875000 505.125000 -576.000000 

point 8 111.968750 511.906250 -584.000000 

point 9 125.781250 511.906250 -584.000000 

point 10 124.468750 504.593750 -448.000000 

point 11 291.343750 511.937500 -456.000000 

point 12 418.656250 511.375000 -456.000000 

point 13 482.468750 511.687500 -456.000000 

point 14 480.468750 432.000000 -448.000000 

point 15 480.687500 436.375000 -368.000000 

point 16 344.843750 437.562500 -368.000000 

point 17 349.562500 518.875000 -368.000000 

point 18 346.093750 598.812500 -368.000000 

point 19 347.312500 670.656250 -368.000000 

point 20 193.906250 678.156250 -368.000000 

point 21 81.718750 677.687500 -368.000000 

point 22 -70.906250 677.000000 -368.000000 

point 23 -67.937500 748.156250 -368.000000 

point 24 -64.468750 578.406250 -368.000000 

point 25 -296.218750 570.156250 -368.000000 

point 26 -349.593750 569.437500 -368.000000 

point 27 -346.875000 648.375000 -368.000000 

point 28 -245.812500 711.125000 -376.000000 

point 29 -246.062500 706.593750 -200.000000 

point 30 -78.562500 706.250000 -200.000000 

point 31 17.093750 705.812500 -200.000000 

point 32 23.500000 777.343750 -200.000000 

point 33 182.968750 776.750000 -200.000000 

point 34 178.406250 672.250000 -200.000000 

point 35 330.156250 679.531250 -208.000000 

point 36 329.343750 567.062500 -208.000000 

point 37 486.718750 558.281250 -208.000000 

point 38 342.031250 556.562500 -88.000000 

point 39 233.625000 661.031250 -88.000000 

point 40 41.437500 660.843750 -88.000000 

point 41 -100.312500 771.968750 -88.000000 

point 42 -96.937500 810.937500 -88.000000 

point 43 -62.437500 762.031250 56.000000 

point 44 120.875000 767.531250 136.000000 

point 45 48.093750 767.093750 120.000000

9.2  Korrespondierende 2-D-Punkte im u,v\protect - Kamerakoordinatensystem der Kamera 1

# Kamerakalibrierungsdatei Kamera #1 Name: cam1 

# Verlassen von umacs mit ctrl-X-C 

imagepoint 1 249 117 

imagepoint 2 238 124 

imagepoint 3 183 122 

imagepoint 4 181 138 

imagepoint 5 119 133 

imagepoint 6 109 173 

imagepoint 7 265 151 

imagepoint 8 361 157 

imagepoint 9 364 158 

imagepoint 10 381 163 

imagepoint 11 455 167 

imagepoint 12 507 171 

imagepoint 13 534 173 

imagepoint 14 529 190 

imagepoint 15 544 193 

imagepoint 16 488 190 

imagepoint 17 497 169 

imagepoint 18 499 151 

imagepoint 19 505 133 

imagepoint 20 437 126 

imagepoint 21 389 122 

imagepoint 22 315 116 

imagepoint 23 322 99 

imagepoint 24 312 140 

imagepoint 25 197 137 

imagepoint 26 169 133 

imagepoint 27 178 115 

imagepoint 28 230 102 

imagepoint 29 247 105 

imagepoint 30 337 112 

imagepoint 31 381 114 

imagepoint 32 390 94 

imagepoint 33 468 103 

imagepoint 34 457 130 

imagepoint 35 528 133 

imagepoint 36 520 162 

imagepoint 37 585 169 

imagepoint 38 548 169 

imagepoint 39 506 137 

imagepoint 40 410 129 

imagepoint 41 340 92 

imagepoint 42 347 83 

imagepoint 43 386 99 

imagepoint 44 504 106 

imagepoint 45 460 103

9.3  Ergebnis der Kameraeichung Kamera 1

* Calibration Data:   cam1.out.txt  

channel      0

gain         -268439016

offset       -277038608

uvoffset     0

calib_status 2

Calibration Data

0.552931921      0.043645239      0.008009932    351.011493523 

0.054124827     -0.282566678     -0.030235412    309.789776375 

0.000121412     -0.000083478     -0.000384610      1.000000000 

Lens Distortion Parameters

Ucomp                       Vcomp

2.03860607994310e+01     -3.43334553287294e+01

1.12647458142566e+00      1.69947432121952e-01

-7.28612313239068e-01      1.18521323159028e+00

-4.09557073689629e-04     -1.59631543110517e-04

1.83528306429403e-04     -1.43193707703679e-03

4.85611194716187e-03      1.24440554271993e-03

4.07615599798360e-07      3.89633616729293e-08

-1.53621820499783e-08      6.89060344730839e-07

-1.36590153617876e-06      2.95095437289277e-06

-9.01754883540607e-06     -6.79533798966758e-06

0.00000000000000e+00      0.00000000000000e+00

0.00000000000000e+00      0.00000000000000e+00

0.00000000000000e+00      0.00000000000000e+00

0.00000000000000e+00      0.00000000000000e+00

0.00000000000000e+00      0.00000000000000e+00

0.00000000000000e+00      0.00000000000000e+00

0.00000000000000e+00      0.00000000000000e+00

0.00000000000000e+00      0.00000000000000e+00

Calibration Accuracy Data - all units are in 'pixels'

1st Col is observed image position

2nd Col is corrected image position

3rd Col is ideal image position

4th Col is difference between observed and ideal image positions

5th Col is difference between compensated and ideal image positions

1    249.000     249.143     251.128    -2.12775    -1.98501    

     117.000     116.849     115.708     1.29175     1.14094    

2    238.000     238.220     239.219    -1.21921    -0.99951    

     124.000     124.121     124.276    -0.27593    -0.15501    

3    183.000     182.641     183.298    -0.29846    -0.65768    

     122.000     121.322     120.163     1.83742     1.15924    

4    181.000     181.317     178.114     2.88621     3.20276    

     138.000     138.348     137.294     0.70558     1.05337    

5    119.000     117.104     117.192     1.80779    -0.08865    

     133.000     132.200     133.114    -0.11445    -0.91411    

6    109.000     110.405     110.475    -1.47452    -0.06918    

     173.000     173.487     173.342    -0.34177     0.14533    

7    265.000     266.311     266.112    -1.11171     0.19916    

     151.000     152.001     153.259    -2.25914    -1.25842    

8    361.000     361.189     360.181     0.81886     1.00755    

     157.000     157.701     157.979    -0.97914    -0.27825    

9    364.000     364.178     366.056    -2.05621    -1.87848    

     158.000     158.669     158.382    -0.38232     0.28629    

10    381.000     381.078     382.669    -1.66910    -1.59126    

      163.000     163.471     163.705    -0.70521    -0.23424    

11    455.000     454.376     454.441     0.55898    -0.06504    

      167.000     167.065     166.684     0.31647     0.38177    

12    507.000     506.656     507.946    -0.94636    -1.29032    

      171.000     170.847     170.457     0.54349     0.39082    

13    534.000     534.170     534.285    -0.28475    -0.11471    

      173.000     172.803     172.177     0.82314     0.62608    

14    529.000     528.585     529.011    -0.01071    -0.42564    

      190.000     189.237     190.253    -0.25281    -1.01593    

15    544.000     543.756     543.974     0.02639    -0.21719    

      193.000     192.208     192.208     0.79178    -0.00064    

16    488.000     487.220     486.396     1.60426     0.82388    

      190.000     189.013     188.285     1.71452     0.72788    

17    497.000     496.539     494.445     2.55546     2.09445    

      169.000     168.906     169.392    -0.39241    -0.48638    

18    499.000     498.531     498.925     0.07527    -0.39410    

      151.000     151.096     150.361     0.63927     0.73543    

19    505.000     504.688     504.891     0.10929    -0.20303    

      133.000     133.013     133.198    -0.19763    -0.18455    

20    437.000     435.971     437.432    -0.43184    -1.46075    

      126.000     126.408     126.108    -0.10849     0.29994    

21    389.000     388.135     386.183     2.81678     1.95175    

      122.000     122.542     122.248    -0.24791     0.29421    

22    315.000     314.817     314.382     0.61751     0.43424    

      116.000     116.317     116.852    -0.85199    -0.53477    

23    322.000     322.350     320.454     1.54628     1.89596    

       99.000      98.817      98.835     0.16549    -0.01757    

24    312.000     312.242     311.087     0.91288     1.15522    

      140.000     140.897     141.870    -1.86953    -0.97211    

25    197.000     197.482     197.698    -0.69786    -0.21610    

      137.000     137.434     135.898     1.10237     1.53676    

26    169.000     168.793     170.809    -1.80931    -2.01608    

      133.000     132.929     134.173    -1.17323    -1.24452    

27    178.000     177.424     176.566     1.43375     0.85728    

      115.000     113.647     113.779     1.22108    -0.13218    

28    230.000     230.358     230.356    -0.35646     0.00188    

      102.000     100.597     101.301     0.69909    -0.70343    

29    247.000     247.318     247.144    -0.14363     0.17465    

      105.000     104.105     104.102     0.89828     0.00330    

30    337.000     336.695     333.980     3.02019     2.71482    

      112.000     112.300     111.086     0.91415     1.21405    

31    381.000     380.307     381.997    -0.99707    -1.68993    

      114.000     114.438     115.014    -1.01379    -0.57598    

32    390.000     390.328     390.518    -0.51837    -0.19073    

       94.000      94.265      96.028    -2.02809    -1.76316    

33    468.000     467.991     468.416    -0.41597    -0.42450    

      103.000     103.257     102.733     0.26687     0.52422    

34    457.000     456.028     457.950    -0.94998    -1.92196    

      130.000     130.319     130.017    -0.01655     0.30269    

35    528.000     528.327     528.099    -0.09854     0.22888    

      133.000     132.844     133.479    -0.47860    -0.63440    

36    520.000     519.940     518.530     1.47036     1.41042    

      162.000     161.955     161.909     0.09089     0.04554    

37    585.000     587.287     588.413    -3.41289    -1.12632    

      169.000     168.888     169.037    -0.03675    -0.14848    

38    548.000     548.655     547.878     0.12205     0.77738    

      169.000     168.857     168.816     0.18387     0.04124    

39    506.000     505.678     504.788     1.21183     0.88974    

      137.000     137.025     137.345    -0.34464    -0.32007    

40    410.000     409.003     408.719     1.28075     0.28421    

      129.000     129.550     130.080    -1.07980    -0.52944    

41    340.000     340.758     343.215    -3.21484    -2.45670    

       92.000      91.837      92.861    -0.86068    -1.02374    

42    347.000     348.679     347.975    -0.97479     0.70448    

       83.000      82.805      81.791     1.20888     1.01341    

43    386.000     385.958     385.989     0.01105    -0.03139    

       99.000      99.270      98.529     0.47063     0.74034    

44    504.000     504.526     503.660     0.34041     0.86669    

      106.000     106.045     106.136    -0.13573    -0.09030    

45    460.000     459.890     460.052    -0.05158    -0.16114 

      103.000     103.284     102.729     0.27075     0.55486 

Uncompensated Data

Mean Squared U error 2.148995

Mean Squared V error 0.835122

Compensated Data

Mean Squared U error 1.602255

Mean Squared V error 0.541317

9.4  Interpretation des Kalibrierungsergebnisses für Kamera 1

Die ermittelte Kameramatrix (vergl. auch Formel 5.6) für Kamera 1 lautet also:

Für die unkompensierten u- und v- Koordinaten ergibt sich ein höherer mittlerer quadratischer Fehler in der Abweichung zu idealen Werten als für den Fall mit Berücksichtigung der Kompensation für die Linsenverzerrung.

Die Fehler (in Pixeln) sind recht klein, die Kalibrierung ist also für diese Kamera erfolgreich durchgrführt worden.

9.5  Korrespondierende 2-D-Punkte im u,v\protect - Kamerakoordinatensystem der Kamera 2

# Kamerakalibrierungsdatei Kamera #2  Name: cam2

# Verlassen von umacs mit ctrl-X-C

imagepoint 1 147 124

imagepoint 2 168 131

imagepoint 3 121 129

imagepoint 4 120 144

imagepoint 5 70 140

imagepoint 6 65 175

imagepoint 7 194 157

imagepoint 8 285 163

imagepoint 9 289 163

imagepoint 10 272 168

imagepoint 11 348 173

imagepoint 12 406 178

imagepoint 13 436 181

imagepoint 14 431 199

imagepoint 15 425 202

imagepoint 16 362 197

imagepoint 17 369 176

imagepoint 18 369 156

imagepoint 19 374 137

imagepoint 20 301 130

imagepoint 21 252 127

imagepoint 22 182 122

imagepoint 23 187 106

imagepoint 24 182 145

imagepoint 25 85 142

imagepoint 26 62 139

imagepoint 27 69 123

imagepoint 28 109 111

imagepoint 29 74 112

imagepoint 30 151 117

imagepoint 31 192 119

imagepoint 32 199 99

imagepoint 33 276 106

imagepoint 34 268 133

imagepoint 35 346 136

imagepoint 36 341 167

imagepoint 37 419 175

imagepoint 38 329 174

imagepoint 39 278 140

imagepoint 40 181 132

imagepoint 41 116 98

imagepoint 42 121 89

imagepoint 43 102 104

imagepoint 44 178 107

imagepoint 45 140 105

9.6  Ergebnis der Kameraeichung Kamera 2

* Calibration Data:   cam2.out.txt  

channel      0

gain         -268439016

offset       -277038608

uvoffset     0

calib_status 2

Calibration Data

0.446308123      0.026567568     -0.260531256    115.713461713 

0.013048250     -0.275414834     -0.039096409    306.967096760 

-0.000150457     -0.000093997     -0.000391016      1.000000000 

Lens Distortion Parameters

Ucomp                       Vcomp

7.40847754796773e+00      7.24054619910675e+00

1.03394493471750e+00      1.14520314457303e-01

-2.02925897804731e-01      6.18317667225794e-01

-5.81956303613890e-04     -1.44951954946166e-04

1.36338197708643e-03     -9.84301591884372e-04

4.44882718357835e-04      3.71358606048348e-03

5.15619029352175e-07      3.04789780004741e-08

1.60228820749051e-06      6.63364394556838e-07

-7.68042610447870e-06      2.08049874119473e-06

2.87379984852855e-06     -1.00881006369262e-05

0.00000000000000e+00      0.00000000000000e+00

0.00000000000000e+00      0.00000000000000e+00

0.00000000000000e+00      0.00000000000000e+00

0.00000000000000e+00      0.00000000000000e+00

0.00000000000000e+00      0.00000000000000e+00

0.00000000000000e+00      0.00000000000000e+00

0.00000000000000e+00      0.00000000000000e+00

0.00000000000000e+00      0.00000000000000e+00

Calibration Accuracy Data - all units are in 'pixels'

1st Col is observed image position

2nd Col is corrected image position

3rd Col is ideal image position

4th Col is difference between observed and ideal image positions

5th Col is difference between compensated and ideal image positions

1    147.000     147.403     149.556    -2.55587    -2.15291    

     124.000     124.115     122.840     1.15969     1.27469    

2    168.000     168.429     169.629    -1.62928    -1.19992    

     131.000     131.371     131.277    -0.27694     0.09427    

3    121.000     121.146     122.534    -1.53441    -1.38831    

     129.000     129.012     128.051     0.94890     0.96105    

4    120.000     120.348     119.093     0.90735     1.25530    

     144.000     144.412     143.533     0.46683     0.87870    

5     70.000      69.228      70.820    -0.81953    -1.59108    

     140.000     139.890     140.031    -0.03087    -0.14135    

6     65.000      67.216      67.273    -2.27269    -0.05637    

     175.000     175.384     175.285    -0.28484     0.09926    

7    194.000     194.350     194.711    -0.71147    -0.36111    

     157.000     157.685     158.354    -1.35396    -0.66854    

8    285.000     284.331     284.889     0.11136    -0.55803    

     163.000     163.385     163.551    -0.55130    -0.16671    

9    289.000     288.312     290.707    -1.70679    -2.39458    

     163.000     163.368     163.999    -0.99917    -0.63158    

10    272.000     271.308     271.762     0.23816    -0.45398    

      168.000     168.373     168.738    -0.73831    -0.36510    

11    348.000     347.220     348.089    -0.08892    -0.86936    

      173.000     173.012     172.690     0.31004     0.32171    

12    406.000     406.695     407.546    -1.54560    -0.85088    

      178.000     177.803     177.483     0.51745     0.32018    

13    436.000     438.220     438.193    -2.19300     0.02701    

      181.000     180.764     179.805     1.19543     0.95957    

14    431.000     431.176     431.474    -0.47412    -0.29830    

      199.000     198.329     199.357    -0.35668    -1.02773    

15    425.000     424.466     424.740     0.26007    -0.27371    

      202.000     201.129     201.292     0.70758    -0.16308    

16    362.000     359.846     358.862     3.13847     0.98450    

      197.000     196.109     195.401     1.59907     0.70794    

17    369.000     368.487     365.829     3.17089     2.65767    

      176.000     175.904     175.544     0.45553     0.35953    

18    369.000     369.227     368.855     0.14494     0.37217    

      156.000     155.939     155.426     0.57443     0.51341    

19    374.000     374.263     373.727     0.27307     0.53591    

      137.000     136.743     137.252    -0.25246    -0.50971    

20    301.000     300.565     300.814     0.18607    -0.24903    

      130.000     130.268     130.460    -0.46024    -0.19257    

21    252.000     251.887     249.148     2.85153     2.73859    

      127.000     127.446     127.143    -0.14289     0.30263    

22    182.000     182.443     181.432     0.56779     1.01120    

      122.000     122.316     122.807    -0.80713    -0.49107    

23    187.000     187.515     185.593     1.40651     1.92189    

      106.000     106.358     105.569     0.43098     0.78922    

24    182.000     182.395     180.293     1.70676     2.10136    

      145.000     145.617     146.659    -1.65939    -1.04288    

25     85.000      84.726      83.298     1.70247     1.42804    

      142.000     142.109     141.391     0.60929     0.71813    

26     62.000      60.911      61.849     0.15133    -0.93759    

      139.000     138.758     139.953    -0.95278    -1.19438    

27     69.000      67.760      65.192     3.80832     2.56792    

      123.000     122.132     121.797     1.20307     0.33525    

28    109.000     109.043     109.973    -0.97321    -0.93037    

      111.000     110.392     109.747     1.25273     0.64471    

29     74.000      72.986      73.200     0.80020    -0.21385    

      112.000     110.776     111.526     0.47400    -0.75041    

30    151.000     151.476     148.021     2.97898     3.45517    

      117.000     117.035     116.496     0.50420     0.53890    

31    192.000     192.414     192.414    -0.41353     0.00033    

      119.000     119.346     119.508    -0.50829    -0.16236    

32    199.000     199.402     198.642     0.35767     0.75946    

       99.000      99.619     100.840    -1.83971    -1.22104    

33    276.000     275.205     276.288    -0.28816    -1.08303    

      106.000     106.711     105.604     0.39571     1.10687    

34    268.000     267.766     268.480    -0.47966    -0.71374    

      133.000     133.415     133.546    -0.54631    -0.13111    

35    346.000     345.792     346.471    -0.47103    -0.67872    

      136.000     135.973     136.657    -0.65676    -0.68366    

36    341.000     340.375     339.260     1.73996     1.11499    

      167.000     167.102     166.809     0.19072     0.29303    

37    419.000     420.549     420.628    -1.62826    -0.07935    

      175.000     174.790     175.478    -0.47796    -0.68758    

38    329.000     327.968     328.892     0.10781    -0.92376    

      174.000     174.059     173.629     0.37102     0.42973    

39    278.000     277.693     277.947     0.05289    -0.25393    

      140.000     140.403     140.214    -0.21426     0.18896    

40    181.000     181.400     180.829     0.17113     0.57156    

      132.000     132.435     133.472    -1.47246    -1.03752    

41    116.000     116.466     117.079    -1.07916    -0.61298    

       98.000      97.391      98.765    -0.76459    -1.37398    

42    121.000     121.807     120.194     0.80612     1.61330    

       89.000      88.622      88.200     0.79970     0.42124    

43    102.000     102.027     102.092    -0.09177    -0.06505    

      104.000     103.141     102.731     1.26881     0.40971    

44    178.000     178.568     180.528    -2.52769    -1.95991    

      107.000     107.265     107.226    -0.22567     0.03903    

45    140.000     140.578     144.545    -4.54470    -3.96654    

      105.000     104.811     104.876     0.12406    -0.06535    

Uncompensated Data

Mean Squared U error 2.797268

Mean Squared V error 0.678343

Compensated Data

Mean Squared U error 2.120540

Mean Squared V error 0.454559

9.7  Interpretation des Kalibrierungsergebnisses für Kamera 2

0.446308123 0.026567568 -0.260531256 115.713461713

0.013048250     -0.275414834     -0.039096409    306.967096760 

-0.000150457     -0.000093997     -0.000391016      1.000000000 

Die ermittelte Kameramatrix (vergl. auch Formel 5.6) für Kamera 2 lautet also:

Für die unkompensierten u- und v- Koordinaten ergibt sich ein höherer mittlerer quadratischer Fehler in der Abweichung zu idealen Werten als für den Fall mit Berücksichtigung der Kompensation für die Linsenverzerrung.

Die Fehler (in Pixeln) sind für diese Kamera etwas größer als für Kamera 1, aber in ihrer Größenordnung ebenfalls recht klein, die Kalibrierung ist also auch für diese Kamera erfolgreich gewesen.

9.8  Evaluation der Stereo-Bildverarbeitung mit 3-D-Daten

Um eine Überprüfung der Genauigkeit der Stereo-Bildverarbeitung vornehmen zu können ist eine Kontrollfunktion in das Steuerprogramm integriert worden. Diese Kontrollfunktion liest ein 3-D-Koordinatenfile ein und führt eine Eichkontrollfahrt mit am Industrieroboter befestigter Eichmarke durch. An jedem spezifizierten Punkt der Eichkontrollfahrt wird die Position des TCP mit der Position, die die Bildverarbeitung generiert hat verglichen. Die so gewonnenen Daten werden in folgendem Format in eine Kontrolldatei geschrieben:

x-Position, y-Position, z-Position des TCP, x-Position, y-Position, z-Position, beobachtet durch die Bildverarbeitung, delta-x delta-y, delta-z Differenz zwischen beobachteter und realer 3-D-Position.

9.8.1  Die 3-D-Koordinaten der Eichkontrollfahrt

Die Eichkontrollfahrt wurde so ,,geteacht'', daß ein möglichst großer Bereich des Arbeitsraums überstrichen wird.

# Eichkontrollfahrt fuer 3-D-Kamerakalibrierung, erzeugt mit Teach-Eichfahrt.

# Verlassen von umacs mit ctrl-X-C

# point N X Y Z

point 1 -112.250000 814.906250 0.000000

point 2 -112.062500 694.687500 0.000000

point 3 -117.750000 558.937500 0.000000

point 4 65.687500 550.843750 0.000000

point 5 217.781250 551.187500 0.000000

point 6 352.875000 551.656250 0.000000

point 7 359.187500 678.875000 0.000000

point 8 190.031250 781.312500 0.000000

point 9 -267.093750 780.437500 0.000000

point 10 -268.375000 700.156250 0.000000

point 11 -268.187500 564.187500 0.000000

point 12 -270.812500 468.406250 0.000000

point 13 -319.531250 543.218750 -152.000000

point 14 -175.906250 542.687500 -152.000000

point 15 -31.625000 541.218750 -152.000000

point 16 420.437500 524.218750 -152.000000

point 17 411.187500 666.031250 -192.000000

point 18 415.593750 484.468750 -296.000000

point 19 406.125000 485.250000 -400.000000

point 20 180.187500 486.312500 -416.000000

point 21 182.406250 573.750000 -416.000000

point 22 71.468750 604.437500 -416.000000

point 23 -104.437500 604.125000 -416.000000

point 24 -243.218750 607.156250 -424.000000

point 25 -412.375000 606.406250 -424.000000

point 26 -421.218750 518.062500 -424.000000

point 27 -416.218750 469.187500 -424.000000

point 28 -418.125000 470.250000 -504.000000

point 29 -421.093750 510.281250 -504.000000

point 30 -307.843750 518.968750 -504.000000

point 31 -147.937500 519.187500 -504.000000

point 32 -147.250000 607.343750 -504.000000

point 33 48.906250 608.593750 -496.000000

point 34 168.781250 608.593750 -496.000000

point 35 326.062500 568.781250 -512.000000

point 36 250.968750 571.562500 -576.000000

point 37 -47.437500 570.406250 -576.000000

point 38 -135.968750 575.093750 -568.000000

point 39 -129.312500 604.656250 -568.000000

point 40 -185.812500 604.281250 -568.000000

point 41 -234.687500 603.843750 -568.000000

9.8.2  Die Eichkontrolldatei